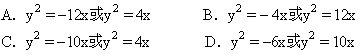摘要：抛物线的顶点在原点.焦点在x轴的正半轴上.直线x+y-1=0与抛物线相交于A.B两点.且|AB|=. (1)求抛物线的方程, (2)在x轴上是否存在一点C.使△ABC为正三角形?若存在.求出C点的坐标:若不存在.请说明理由. 解:(1)设所求抛物线方程为. 则由消支y得 x2-2(1+p)x+1=0 设A(x1.y1).B(x2.y2) 则x1+ x2＝2(1+p) x1x2＝1 由弦长|AB|=建立关于p的方程. 解得 p=或p=- 故抛物线方程为. (2)设AB的中点为D则D(.-).x轴上存在满足条件的点C(x0,0). 由于△ABC为正三角形.所以CD⊥AB.|CD|=|AB|=. 由CD⊥AB得x0＝ 但|CD|＝|AB|= 故x轴上不存在点C.使△ABC为正三角形.

网址：http://m.1010jiajiao.com/timu3_id_516841[举报]