摘要:函数的极值 ①极值定义:如果函数在点附近有定义.那么对附近的点.都有<我们就说函数的一个极大值.记作=, 在点附近的点.都有>我们就说函数的一个极小值.记作=,极大值与极小值统称为极值. ②极值判别法:当函数在点处连续时.极值判断法是: 如果在附近的左侧>0.右侧<0.那么是极大值, 如果在附近的左侧<0.右侧>0.那么是极小值. ③求可导函数极值的步骤: 首先:求导数,再求导数=0的根,最后:检查在方程根左右的值的符号.如果左正右负.那么在这个根处取极大值,如果左负右正.那么在这个根处取极小值. 说明:曲线在处有极值.可以说明以下四个内容: ①点在曲线上.满足,②该处导数=0, ③是方程的根, ④.符号各异. 9函数的最大值与最小值 在闭区间[]上连续.在()内可导.在[]上求最大值与最小值的步骤: 先求在()内的极值,再将的各极值与.比较.其中最大的一个是最大值.最小的一个是最小值. 说明:利用导数求最值的步骤: (1)求导数, (2)求方程=0的根 (3)计算极值及端点函数值的大小,(4)根据上述值的大小,确定最大值与最小值.
网址:http://m.1010jiajiao.com/timu3_id_516668[举报]
设定义在R上的函数f(x)=a0x4+a1x3+a2x2+a3x+a4,a0,a1,a2,a3,a4∈R,当x=-1时,f(x)取得极大值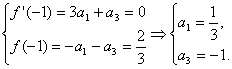 ,且函数y=f(x+1)的图象关于点(-1,0)对称.
,且函数y=f(x+1)的图象关于点(-1,0)对称.
(1)求f(x)的表达式;
(2)在函数y=f(x)的图象上是否存在两点,使以这两点为切点的切线互相垂直,且切点的横坐标都在[![]() ,
,![]() ]上?如果存在,求出这两点的坐标;如果不存在,请说明理由;
]上?如果存在,求出这两点的坐标;如果不存在,请说明理由;
(3)设xn=![]() ,ym=
,ym=![]() (m,n∈N*),求证:|f(xn)-f(ym)|<
(m,n∈N*),求证:|f(xn)-f(ym)|<![]() .
.
设定义在R上的函数f(x)=ax4+a1x3+a2x2+a3x+a4,a,a1,a2,a3,a4∈R,当x=-1时,f(x)取得极大值 ,且函数y=f(x+1)的图象关于点(-1,0)对称.
,且函数y=f(x+1)的图象关于点(-1,0)对称.
(Ⅰ)求f(x)的表达式;
(Ⅱ)在函数y=f(x)的图象上是否存在两点,使以这两点为切点的切线互相垂直,且切点的横坐标都在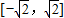 上?如果存在,求出点的坐标;如果不存在,请说明理由;
上?如果存在,求出点的坐标;如果不存在,请说明理由;
(Ⅲ)设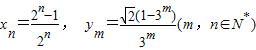 ,求证:
,求证: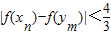 .
.
查看习题详情和答案>>
 ,且函数y=f(x+1)的图象关于点(-1,0)对称.
,且函数y=f(x+1)的图象关于点(-1,0)对称.(Ⅰ)求f(x)的表达式;
(Ⅱ)在函数y=f(x)的图象上是否存在两点,使以这两点为切点的切线互相垂直,且切点的横坐标都在
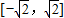 上?如果存在,求出点的坐标;如果不存在,请说明理由;
上?如果存在,求出点的坐标;如果不存在,请说明理由;(Ⅲ)设
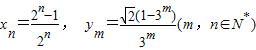 ,求证:
,求证: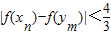 .
.查看习题详情和答案>>
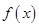 为定义在R上的偶函数,且导数
为定义在R上的偶函数,且导数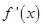 存在,则
存在,则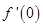 的值为 ( ▲ )
的值为 ( ▲ )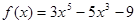 的极值点的个数( ▲ )
的极值点的个数( ▲ ) ,且函数y=f(x+1)的图象关于点(-1,0)对称.
,且函数y=f(x+1)的图象关于点(-1,0)对称.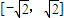 上?如果存在,求出点的坐标;如果不存在,请说明理由;
上?如果存在,求出点的坐标;如果不存在,请说明理由;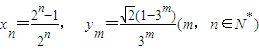 ,求证:
,求证: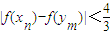 .
.