摘要:考试要求:1.掌握椭圆的定义.标准方程和椭圆的简单几何性质.理解椭圆的参数方程.2.掌握双曲线的定义.标准方程和双曲线的简单几何性质.3.掌握抛物线的定义.标准方程和抛物线的简单几何性质.4.了解圆锥曲线的初步应用.
网址:http://m.1010jiajiao.com/timu3_id_516602[举报]
椭圆的中心是原点O,它的短轴长为2
,相应于焦点F(c,0)(c>0)的准线l与x轴相交于点A,|OF|=2|FA|,过点A的直线与椭圆相交于P、Q两点.
(1)求椭圆的方程及离心率;
(2)若
•
=0,求直线PQ的方程.
查看习题详情和答案>>
| 2 |
(1)求椭圆的方程及离心率;
(2)若
| OP |
| OQ |
已知椭圆
+
=1(a>0,b>0)与双曲线x2-y2=1有共同的焦点F1、F2,设它们在第一象限的交点为P,且PF1⊥PF2
(1)求椭圆的方程;
(2)已知N(0,-1),对于(1)中的椭圆,是否存在斜率为k(k≠0)的直线l,与椭圆交于不同的两点A、B,点Q满足
=
,且
•
=0?若存在,求出k的取值范围;若不存在,说明理由.
查看习题详情和答案>>
| x2 |
| a2 |
| y2 |
| b2 |
(1)求椭圆的方程;
(2)已知N(0,-1),对于(1)中的椭圆,是否存在斜率为k(k≠0)的直线l,与椭圆交于不同的两点A、B,点Q满足
| AQ |
| QB |
| NQ |
| AB |
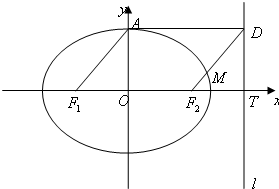 如图,已知椭圆
如图,已知椭圆