摘要：向量的表示方法: (1)几何表示法:用带箭头的有向线段表示.如.注意起点在前.终点在后, (2)符号表示法:用一个小写的英文字母来表示.如..等, (3)坐标表示法:在平面内建立直角坐标系.以与轴.轴方向相同的两个单位向量.为基底.则平面内的任一向量可表示为 .称为向量的坐标.＝叫做向量的坐标表示.如果向量的起点在原点.那么向量的坐标与向量的终点坐标相同.
网址：http://m.1010jiajiao.com/timu3_id_516555[举报]
在平面直角坐标系中，对其中任何一向量
，定义范数
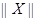，它满足以下性质：⑴
，当且仅当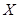
为零向量时，不等式取等号；⑵对任意的实数
， 
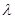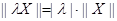（注：此处点乘号为普通的乘号）；⑶
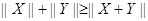．应用类比的方法，我们可以给出空间直角坐标系下范数的定义，现有空间向量
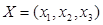，下面给出的几个表达式中，可能表示向量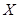的范数的是
（把所有正确答案的序号都填上）
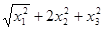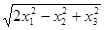⑴
⑵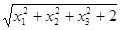 
⑶
⑷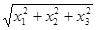
查看习题详情和答案>>
在平面直角坐标系中，对其中任何一向量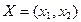
，定义范数
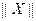，它满足以下性质：⑴
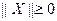，当且仅当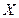
为零向量时，不等式取等号；⑵对任意的实数
，
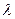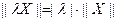（注：此处点乘号为普通的乘号）；⑶
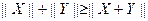．应用类比的方法，我们可以给出空间直角坐标系下范数的定义，现有空间向量
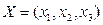，下面给出的几个表达式中，可能表示向量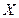的范数的是
（把所有正确答案的序号都填上）
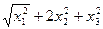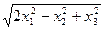⑴
⑵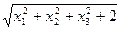
⑶
⑷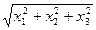
在平面直角坐标系中，对其中任何一向量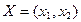
，定义范数
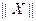，它满足以下性质：⑴
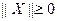，当且仅当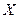
为零向量时，不等式取等号；⑵对任意的实数
，
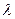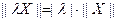（注：此处点乘号为普通的乘号）；⑶
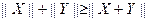．应用类比的方法，我们可以给出空间直角坐标系下范数的定义，现有空间向量
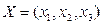，下面给出的几个表达式中，可能表示向量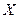的范数的是
（把所有正确答案的序号都填上）
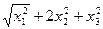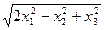⑴
⑵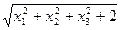
⑶
⑷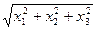
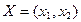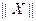，定义范数，它满足以下性质：⑴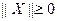，当且仅当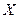为零向量时，不等式取等号；⑵对任意的实数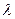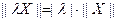，（注：此处点乘号为普通的乘号）；⑶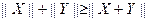．应用类比的方法，我们可以给出空间直角坐标系下范数的定义，现有空间向量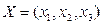，下面给出的几个表达式中，可能表示向量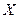的范数的是（把所有正确答案的序号都填上）
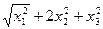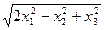⑴
⑵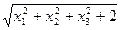 ⑶ ⑷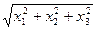
在平面直角坐标系中，对其中任何一向量X=（x1，x2），定义范数||X||，它满足以下性质：（1）||X||≥0，当且仅当X为零向量时，不等式取等号；（2）对任意的实数λ，||λX||=|λ|•||X||（注：此处点乘号为普通的乘号）；（3）||X||+||Y||≥||X+Y||．应用类比的方法，我们可以给出空间直角坐标系下范数的定义，现有空间向量X=（x1，x2，x3），下面给出的几个表达式中，可能表示向量X的范数的是 （把所有正确答案的序号都填上）
（1）
+2x22+x32（2）
（3）
（4）
．
查看习题详情和答案>>
（1）
| x12 |
| 2x2-x22+x32 |
| x12+x22+x32+2 |
| x12+x22+x32 |
在平面直角坐标系中，对其中任何一向量X=（x1，x2），定义范数||X||，它满足以下性质：（1）||X||≥0，当且仅当X为零向量时，不等式取等号；（2）对任意的实数λ，||λX||=|λ|•||X||（注：此处点乘号为普通的乘号）；（3）||X||+||Y||≥||X+Y||．应用类比的方法，我们可以给出空间直角坐标系下范数的定义，现有空间向量X=（x1，x2，x3），下面给出的几个表达式中，可能表示向量X的范数的是______（把所有正确答案的序号都填上）
（1）
+2x22+x32（2）
（3）
（4）
．
查看习题详情和答案>>
（1）
| x12 |
| 2x2-x22+x32 |
| x12+x22+x32+2 |
| x12+x22+x32 |