摘要:三种圆锥曲线的研究 (1)统一定义.三种圆锥曲线均可看成是这样的点集:.其中F为定点.d为P到定直线的l距离.Fl.如图. 因为三者有统一定义.所以.它们的一些性质.研究它们的一些方法都具有规律性. 当0<e<1时.点P轨迹是椭圆,当e>1时.点P轨迹是双曲线,当e=1时.点P轨迹是抛物线. (2)椭圆及双曲线几何定义:椭圆:{P||PF1|+|PF2|=2a.2a>|F1F2|>0.F1.F2为定点}.双曲线{P|||PF1|-|PF2||=2a.|F1F2|>2a>0.F1.F2为定点}. (3)圆锥曲线的几何性质:几何性质是圆锥曲线内在的.固有的性质.不因为位置的改变而改变. ①定性:焦点在与准线垂直的对称轴上 椭圆及双曲线中:中心为两焦点中点.两准线关于中心对称,椭圆及双曲线关于长轴.短轴或实轴.虚轴成轴对称.关于中心成中心对称. ②定量: 椭 圆 双 曲 线 抛 物 线 焦 距 2c 长轴长 2a -- 实轴长 -- 2a 短轴长 2b 焦点到对应 准线距离 P=2 p 通径长 2· 2p 离心率 1 基本量关系 a2=b2+c2 C2=a2+b2 (4)圆锥曲线的标准方程及解析量 举焦点在x轴上的方程如下: 椭 圆 双 曲 线 抛 物 线 标准方程 y2=2px 顶 点 (0.0) 焦 点 (.0) 准 线 X=± x= 中 心 (0.0) 有界性 |x|≤a |y|≤b |x|≥a x≥0 焦半径 P(x0.y0)为圆锥曲线上一点.F1.F2分别为左.右焦点 |PF1|=a+ex0 |PF2|=a-ex0 P在右支时: |PF1|=a+ex0 |PF2|=-a+ex0 P在左支时: |PF1|=-a-ex0 |PF2|=a-ex0 |PF|=x0+ 总之研究圆锥曲线.一要重视定义.这是学好圆锥曲线最重要的思想方法.二要数形结合.既熟练掌握方程组理论.又关注图形的几何性质.以简化运算.
网址:http://m.1010jiajiao.com/timu3_id_516407[举报]
 成等比数列,则圆锥曲线
成等比数列,则圆锥曲线 的离心率为
的离心率为 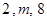 成等比数列,则圆锥曲线
成等比数列,则圆锥曲线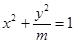 的离心率为
的离心率为  成等比数列,则圆锥曲线
成等比数列,则圆锥曲线 的离心率为
的离心率为