摘要：2．指数函数与对数函数 (1)指数函数: ①定义:函数称指数函数. 1)函数的定义域为R,2)函数的值域为, 3)当时函数为减函数.当时函数为增函数. ②函数图像: 1)指数函数的图象都经过点(0.1).且图象都在第一.二象限, 2)指数函数都以轴为渐近线(当时.图象向左无限接近轴.当时.图象向右无限接近轴), 3)对于相同的.函数的图象关于轴对称. ①. ②. ③ ①. ②. ③. ③函数值的变化特征: (2)对数函数: ①定义:函数称对数函数. 1)函数的定义域为,2)函数的值域为R, 3)当时函数为减函数.当时函数为增函数, 4)对数函数与指数函数互为反函数. ②函数图像: 1)对数函数的图象都经过点(0.1).且图象都在第一.四象限, 2)对数函数都以轴为渐近线(当时.图象向上无限接近轴,当时.图象向下无限接近轴), 4)对于相同的.函数的图象关于轴对称. ③函数值的变化特征: ①. ②. ③. ①. ②. ③.
网址：http://m.1010jiajiao.com/timu3_id_516395[举报]
已知指数函数y=g（x）满足：g(-3)=
，定义域为R的函数f（x）=
是奇函数．
（1）确定函数g（x）与f（x）的解析式；
（2）若对任意的t∈R，不等式f（t2-2t）+f（2t2-k）＜0恒成立，求实数k的取值范围． 查看习题详情和答案>>
| 1 |
| 8 |
| -g(x)+n |
| 2g(x)+m |
（1）确定函数g（x）与f（x）的解析式；
（2）若对任意的t∈R，不等式f（t2-2t）+f（2t2-k）＜0恒成立，求实数k的取值范围． 查看习题详情和答案>>
已知指数函数y=g（x）满足：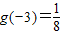
，定义域为R的函数f（x）=
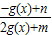是奇函数．
（1）确定函数g（x）与f（x）的解析式；
（2）若对任意的t∈R，不等式f（t2-2t）+f（2t2-k）＜0恒成立，求实数k的取值范围．
查看习题详情和答案>>
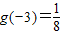，定义域为R的函数f（x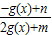）=是奇函数．（1）确定函数g（x）与f（x）的解析式；
（2）若对任意的t∈R，不等式f（t2-2t）+f（2t2-k）＜0恒成立，求实数k的取值范围．
查看习题详情和答案>>
已知指数函数y=g（x）满足：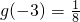
，定义域为R的函数f（x）=
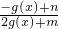是奇函数．
（1）确定函数g（x）与f（x）的解析式；
（2）若对任意的t∈R，不等式f（t2-2t）+f（2t2-k）＜0恒成立，求实数k的取值范围．
查看习题详情和答案>>
已知指数函数y=g（x）满足：g(-3)=
，定义域为R的函数f（x）=
是奇函数．
（1）确定函数g（x）与f（x）的解析式；
（2）若对任意的t∈R，不等式f（t2-2t）+f（2t2-k）＜0恒成立，求实数k的取值范围．
查看习题详情和答案>>
| 1 |
| 8 |
| -g(x)+n |
| 2g(x)+m |
（1）确定函数g（x）与f（x）的解析式；
（2）若对任意的t∈R，不等式f（t2-2t）+f（2t2-k）＜0恒成立，求实数k的取值范围．
已知函数f（x）=mx3+nx2（m、n∈R，m≠0）的图象在（2，f（2））处的切线与x轴平行．
（1）求n，m的关系式并求f（x）的单调减区间；
（2）证明：对任意实数0＜x1＜x2＜1，关于x的方程：f′(x)-
=0在（x1，x2）恒有实数解
（3）结合（2）的结论，其实我们有拉格朗日中值定理：若函数f（x）是在闭区间[a，b]上连续不断的函数，且在区间（a，b）内导数都存在，则在（a，b）内至少存在一点x0，使得f′(x0)=
．如我们所学过的指、对数函数，正、余弦函数等都符合拉格朗日中值定理条件．试用拉格朗日中值定理证明：
当0＜a＜b时，
＜ln
＜
（可不用证明函数的连续性和可导性）．
查看习题详情和答案>>
（1）求n，m的关系式并求f（x）的单调减区间；
（2）证明：对任意实数0＜x1＜x2＜1，关于x的方程：f′(x)-
| f(x2)-f(x1) |
| x2-x1 |
（3）结合（2）的结论，其实我们有拉格朗日中值定理：若函数f（x）是在闭区间[a，b]上连续不断的函数，且在区间（a，b）内导数都存在，则在（a，b）内至少存在一点x0，使得f′(x0)=
| f(b)-f(a) |
| b-a |
当0＜a＜b时，
| b-a |
| b |
| b |
| a |
| b-a |
| a |