摘要：如图所示.曲线段OMB是函数f(x)=x2(0<x<6)的图象.BA⊥x轴于A.曲线段OMB上一点M(t.f(t))处的切线PQ交x轴于P.交线段AB于Q. (1)试用t表示切线PQ的方程, (2)试用t表示△QAP的面积g(t).若函数g(t)在［m.n］上单调递减.试求出m的最小值. 解:(1)(x)=2x. ∴k=2t.切线PQ的方程为 y-t2=2t(x-t).即2tx-y-t2=0. 可求得P(.0).Q(6.12t-t2). ∴g(t)=S△QAP=(6-t)(12t-t2)=t3-6t2+36t(0<t<6).g′(t)=t2-12t+36.令g′(t)<0.得4<t<12. 考虑到0<t<6.∴4<t<6.即g(t)的单调减区间为(4.6). ∴m的最小值为4.
网址：http://m.1010jiajiao.com/timu3_id_516175[举报]
如图所示，曲线段OMB是函数f(x)=x2（0<x<6）的图像，BA^x轴于A，曲线段OMB上一点M(t，f(t))处的切线PQ交x轴于P，交线段AB于Q，
（1）试用t表示切线PQ的方程；
（2）试用t表示出DQAP的面积g(t)；若函数g(t)在(m，n)上单调递减，试求出m的最小值；
（3）若SDQAPÏ[
，64]，试求出点P横坐标的取值范围．
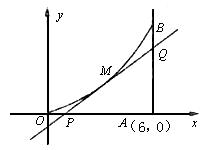
查看习题详情和答案>>
如图所示，曲线段OMB是函数f(x)=x2（0<x<6）的图像，BA^x轴于A，曲线段OMB上一点M(t，f(t))处的切线PQ交x轴于P，交线段AB于Q，
（1）试用t表示切线PQ的方程；
（2）试用t表示出DQAP的面积g(t)；若函数g(t)在(m，n)上单调递减，试求出m的最小值；
（3）若SDQAPÏ[
，64]，试求出点P横坐标的取值范围．
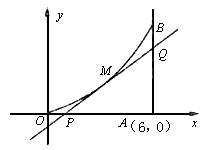
查看习题详情和答案>>
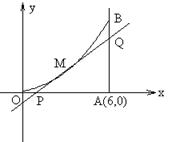
如图所示，曲线段OMB是函数f(x)＝x2(0＜x＜6＝的图象，BA⊥x轴于A，曲线段OMB上一点M(t,f(t))处的切线PQ交x轴于P，交线段AB于Q，⑴试用t表示切线PQ的方程；⑵试用t表示出△QAP的面积g(t)；若函数g(t)在(m，n)上单调递减，试求出m的最小值；⑶若S△QAP∈[
]，试求出点P横坐标的取值范围
，64]，试求出点P横坐标的取值范围．
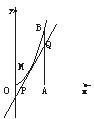如图所示，曲线段OMB是函数f（x）=x2（0＜x＜6）的图象，BA⊥x轴于A，曲线段OMB上一点M（t，f（t））处的切线PQ交x轴于P，交线段AB于Q，