题目内容
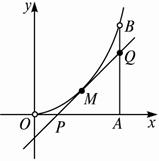
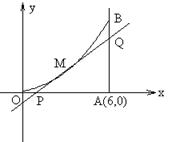
 如图所示,曲线段OMB是函数f(x)=x2(0<x<6)的图象,BA⊥x轴于A,曲线段OMB上一点M(t,f(t))处的切线PQ交x轴于P,交线段AB于Q,
如图所示,曲线段OMB是函数f(x)=x2(0<x<6)的图象,BA⊥x轴于A,曲线段OMB上一点M(t,f(t))处的切线PQ交x轴于P,交线段AB于Q,(1)试用t表示切线PQ的方程;
(2)试用t表示△QAP的面积g(t),若函数g(t)在[m,n]上单调递减,试求出m的最小值.
分析:(1)先对函数f(x)进行求导,根据在M点的导数值为切线的斜率从而得到答案.
(2)先求出点PQ的坐标然后表示出函数g(t)的解析式,再对函数g(t)求导令其导函数小于0即可得到答案.
(2)先求出点PQ的坐标然后表示出函数g(t)的解析式,再对函数g(t)求导令其导函数小于0即可得到答案.
解答:解:(1)f′(x)=2x,
∴k=2t,切线PQ的方程为
y-t2=2t(x-t),即2tx-y-t2=0.
(2)由(1)可求得P(
,0),Q(6,12t-t2),
∴g(t)=S△QAP=
(6-
t)(12t-t2)=
t3-6t2+36t(0<t<6),
g′(t)=
t2-12t+36.令g′(t)<0,得4<t<12.
考虑到0<t<6,∴4<t<6,即g(t)的单调减区间为(4,6).∴m的最小值为4.
∴k=2t,切线PQ的方程为
y-t2=2t(x-t),即2tx-y-t2=0.
(2)由(1)可求得P(
| t |
| 2 |
∴g(t)=S△QAP=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
g′(t)=
| 3 |
| 4 |
考虑到0<t<6,∴4<t<6,即g(t)的单调减区间为(4,6).∴m的最小值为4.
点评:本题主要考查导数的几何意义和函数单调性与其导函数正负之间的关系.属中档题.

练习册系列答案
相关题目
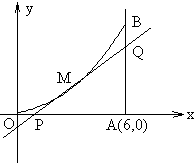 如图所示,曲线段OMB是函数f(x)=x2(0<x<6)的图象,BA⊥x轴于A,曲线段OMB上一点M(t,f(t))处的切线PQ交x轴于P,交线段AB于Q,
如图所示,曲线段OMB是函数f(x)=x2(0<x<6)的图象,BA⊥x轴于A,曲线段OMB上一点M(t,f(t))处的切线PQ交x轴于P,交线段AB于Q,