题目内容
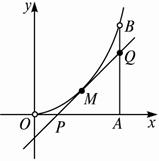
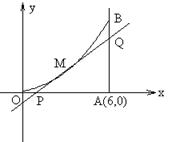
如图所示,曲线段OMB是函数f(x)=x2(0<x<6)的图像,BA⊥x轴于A,曲线段OMB上一点M(t,f(t))处的切线PQ交x轴于P,交线段AB于Q.
(1)试用t表示切线PQ的方程;
(2)试用t表示出△QAP的面积g(t);若函数g(t)在(m,n)上单调递减,试求出m的最小值;
(3)若S△QAP∈[![]() ,64],试求出点P横坐标的取值范围.
,64],试求出点P横坐标的取值范围.

答案:
解析:
解析:
|
解 (1)设点M(t,t2),又 ∴过点M的切线PQ的斜率k=2t, ∴切线PQ的方程为:y=2tx-t2. (2)由(1)可求得,P( ∴g(t)=S△QAP= = 由于 ∴函数g(t)的单调递减区间是(4,6),因此m的最小值为4. (3)由(2)知,g(t)在区间(4,6)上递减,∴此时S△QAP∈(g(6),g(4))=(54,64). 令 S△QAP∈(g(0),g(4))=(0,64),又g(4)=64,∴g(t)的值域为(0,64].由 ∴ |

练习册系列答案
 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案
相关题目
 (x)=2x,
(x)=2x, .
.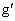 (t)=
(t)=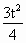 -12t+36,令
-12t+36,令 ≤
≤ <3,∴点P的横坐标∈[
<3,∴点P的横坐标∈[ ,3).
,3).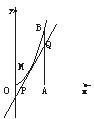 如图所示,曲线段OMB是函数f(x)=x2(0<x<6)的图象,BA⊥x轴于A,曲线段OMB上一点M(t,f(t))处的切线PQ交x轴于P,交线段AB于Q,
如图所示,曲线段OMB是函数f(x)=x2(0<x<6)的图象,BA⊥x轴于A,曲线段OMB上一点M(t,f(t))处的切线PQ交x轴于P,交线段AB于Q,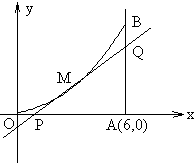 如图所示,曲线段OMB是函数f(x)=x2(0<x<6)的图象,BA⊥x轴于A,曲线段OMB上一点M(t,f(t))处的切线PQ交x轴于P,交线段AB于Q,
如图所示,曲线段OMB是函数f(x)=x2(0<x<6)的图象,BA⊥x轴于A,曲线段OMB上一点M(t,f(t))处的切线PQ交x轴于P,交线段AB于Q,