摘要：分式不等式的解法:分式不等式的一般解题思路是先移项使右边为0.再通分并将分子分母分解因式.并使每一个因式中最高次项的系数为正.最后用标根法求解.解分式不等式时.一般不能去分母.但分母恒为正或恒为负时可去分母.
网址：http://m.1010jiajiao.com/timu3_id_515595[举报]
解不等式：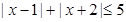 
【解析】本试题主要是考查了分段函数与绝对值不等式的综合运用。利用零点分段论 的思想，分为三种情况韬略得到解集即可。也可以利用分段函数图像来解得。
解：方法一：零点分段讨论：
方法二：数形结合法：
查看习题详情和答案>>
有以下三个不等式：
；
；
．
请你观察这三个不等式，猜想出一个一般性的结论，并证明你的结论。
【解析】根据已知条件可知归纳猜想结论为
下面给出运用综合法的思想求解和证明。解：结论为：． …………………5分
证明：
所以
查看习题详情和答案>>
下列四种说法：
（1）不等式（x-1）
≥0的解集为[2，+∞）；
（2）若a，b∈R，则“log3a＞log3b”是“(
)a＜(
)b”成立的必要不充分条件；
（3）把函数y=sin（-2x）（x∈R）的图象上所有的点向右平移
个单位即可得到函数
y=sin(-2x+
)(x∈R)的图象；
（4）函数f(x)=log
(x2+ax+2)的值域为R，则实数a的取值范围是（-2
，2
）．
其中正确的说法有（ ）
（1）不等式（x-1）
| x2-x-2 |
（2）若a，b∈R，则“log3a＞log3b”是“(
| 1 |
| 3 |
| 1 |
| 3 |
（3）把函数y=sin（-2x）（x∈R）的图象上所有的点向右平移
| π |
| 8 |
y=sin(-2x+
| π |
| 4 |
（4）函数f(x)=log
| 1 |
| 2 |
| 2 |
| 2 |
其中正确的说法有（ ）
| A、.1个 | B、2个 |
| C、3个 | D、.4个 |
0的解集为[2，+∞）；
”成立的必要不充分条件；
个单位即可得到函数
的图象；
的值域为R，则实数a的取值范围是（-2
，2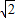
）．