摘要: 设抛物线的焦点为F.准线为l.过点F的直线斜率为k且与抛物线交于A.B两点.P在准线l上. (I)当k=1且直线PA与PB相互垂直时.求点P的坐标, (II)设P(k,),试问是否存在常数.使等式恒成立?若存在.求出的值,若不存在.说明理由.
网址:http://m.1010jiajiao.com/timu3_id_515507[举报]
(本小题满分12分)
 设直线l与抛物线y2=2px(p>0)交于A、B两点,已知当直线l经过抛物线的焦点且与x轴垂直时,△OAB的面积为
设直线l与抛物线y2=2px(p>0)交于A、B两点,已知当直线l经过抛物线的焦点且与x轴垂直时,△OAB的面积为![]() (O为坐标原点).
(O为坐标原点).
(Ⅰ)求抛物线的方程;
(Ⅱ)当直线l经过点P(a,0)(a>0)且与x轴不垂直时,
若在x轴上存在点C,使得△ABC为等边三角形,求a
的取值范围.
查看习题详情和答案>>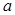 是实数,有下列两个命题:
是实数,有下列两个命题: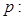 空间两点
空间两点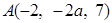 与
与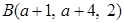 的距离
的距离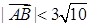 .
.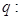 抛物线
抛物线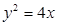 上的点
上的点 到其焦点
到其焦点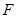 的距离
的距离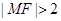 .
.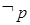 ”和“
”和“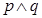 ”都为假命题,求
”都为假命题,求 是实数,有下列两个命题:
是实数,有下列两个命题: 空间两点
空间两点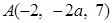 与
与 的距离
的距离 .
. 抛物线
抛物线 上的点
上的点 到其焦点
到其焦点 的距离
的距离 .
.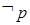 ”和“
”和“ ”都为假命题,求
”都为假命题,求 当△PF1F2的边长恰好是三个连续的自然数时,求抛物线方程;此时设⊙C1、⊙C2……⊙Cn是圆心在
当△PF1F2的边长恰好是三个连续的自然数时,求抛物线方程;此时设⊙C1、⊙C2……⊙Cn是圆心在