摘要:例1.作出下列函数的图象, 解:(1)当x≥2时.即x-2≥0时. 当x<2时.即x-2<0时. 这是分段函数.每段函数图象可根据二次函数图象作出 例2. 解析: . 例3.已知是二次函数.不等式的解集是且在区间上的最大值是12. (I)求的解析式, (II)是否存在实数使得方程在区间内有且只有两个不等的实数根?若存在.求出的取值范围,若不存在.说明理由. 解:(I)是二次函数.且的解集是 可设在区间上的最大值是 由已知.得 (II)方程等价于方程 设则 当时.是减函数,当时.是增函数. 方程在区间内分别有惟一实数根.而在区间内没有实数根.所以存在惟一的自然数使得方程在区间内有且只有两个不同的实数根. 例4:已知二次函数f(x)=ax2+bx+c和一次函数g(x)=-bx.其中a.b.c满足a>b>c,a+b+c=0,(a,b,c∈R)(1)求证两函数的图象交于不同的两点A.B, (2)求线段AB在x轴上的射影A1B1的长的取值范围 解: (1)证明由消去y得ax2+2bx+c=0 Δ=4b2-4ac=4(-a-c)2-4ac=4(a2+ac+c2)=4[(a+c2] ∵a+b+c=0,a>b>c,∴a>0,c<0 ∴c2>0,∴Δ>0,即两函数的图象交于不同的两点 (2)解设方程ax2+bx+c=0的两根为x1和x2,则x1+x2=-,x1x2= |A1B1|2=(x1-x2)2=(x1+x2)2-4x1x2 ∵a>b>c,a+b+c=0,a>0,c<0.∴a>-a-c>c,解得∈(-2,-) ∵的对称轴方程是 ∈(-2,-)时.为减函数 ∴|A1B1|2∈,故|A1B1|∈() 例5:已知f(x)=x2+c,且f[f(x)]=f(x2+1) (1)设g(x)=f[f(x)],求g(x)的解析式,(2)设φ(x)=g(x)-λf(x),试问 是否存在实数λ,使φ(x)在内为减函数.且在内是增函数 点拨与提示:由f[f(x)]=f(x2+1)求出c.进而得到函数的解析式.利用导数研究函数的单调性. 解: (1)由题意得f[f(x)]=f(x2+c)=(x2+c)2+c, f(x2+1)=(x2+1)2+c,∵f[f(x)]=f(x2+1) ∴(x2+c)2+c=(x2+1)2+c,∴x2+c=x2+1,∴c=1 ∴f(x)=x2+1,g(x)=f[f(x)]=f(x2+1)=(x2+1)2+1 (2)φ(x)=g(x)-λf(x)=x4+(2-λ)x2+(2-λ) 若满足条件的λ存在.则φ′(x)=4x3+2(2-λ)x ∵函数φ(x)在上是减函数. ∴当x<-1时.φ′(x)<0 即4x3+2(2-λ)x<0对于x∈恒成立 ∴2(2-λ)>-4x2, ∵x<-1,∴-4x2<-4 ∴2(2-λ)≥-4,解得λ≤4 又函数φ(x)在上是增函数 ∴当-1<x<0时.φ′(x)>0 即4x2+2(2-λ)x>0对于x∈恒成立 ∴2(2-λ)<-4x2, ∵-1<x<0,∴-4<4x2<0 ∴2(2-λ)≤-4,解得λ≥4 故当λ=4时.φ(x)在上是减函数.在上是增函数.即满足条件的λ存在 例6. 已知.t∈[.8].对于f(t)值域内的所有实数m.不等式恒成立.求x的取值范围. 解:∵t∈[.8].∴f(t)∈[.3]原题转化为:>0恒成立.为m的一次函数当x=2时.不等式不成立.∴x≠2.令g(m)=.m∈[.3]问题转化为g(m)在m∈[.3]上恒对于0.则:,解得:x>2或x<-1 例8. 解: 综上所述.得原不等式的解集为 ,, ,, 例9. 若方程上有唯一解. 求m的取值范围. 解:原方程等价于 令.在同一坐标系内.画出它们的图象. 其中注意.当且仅当两函数的图象在[0.3)上有唯一公共点时.原方程有唯一解.由下图可见.当m=1.或时.原方程有唯一解.因此m的取值范围为[-3.0]{1}. 例10.设函数f(x)=ax2+bx+c的图象与两直线y=x.y=x.均不相交.试证明对一切都有. 证明:由题意知.a≠0.设f(x)=a(x-x0)2+f(x0).则 又二次方程ax2+bx+c=±x无实根.故 Δ1=(b+1)2-4ac<0.Δ2=(b-1)2-4ac<0. 所以(b+1)2+(b-1)2-8ac<0.即2b2+2-8ac<0.即b2-4ac<-1.所以|b2-4ac|>1.
网址:http://m.1010jiajiao.com/timu3_id_515303[举报]
解答下列各题:
(1)请作出下列函数的大致图象
①y=
如图1;
②y=log3
如图2.

(2)如图

图甲中阴影部分表示的集合为
图乙表示的函数解析式可以为
查看习题详情和答案>>
(1)请作出下列函数的大致图象
①y=
|
②y=log3
| 1 |
| x+1 |

(2)如图

图甲中阴影部分表示的集合为
(CUB)∩A∪(B∩C)
(CUB)∩A∪(B∩C)
;图乙表示的函数解析式可以为
f(x)=
|
f(x)=
.
|
 某种洗衣机在洗涤衣服时,需经过进水、清洗、排水、脱水四个连续的过程.假设进水时水量匀速增加,清洗时水量保持不变.已知进水时间为4分钟,清洗时间为12分钟,排水时间为2分钟,脱水时间为2分钟.洗衣机中的水量y(升)与时间x(分钟)之间的关系如下表所示:
某种洗衣机在洗涤衣服时,需经过进水、清洗、排水、脱水四个连续的过程.假设进水时水量匀速增加,清洗时水量保持不变.已知进水时间为4分钟,清洗时间为12分钟,排水时间为2分钟,脱水时间为2分钟.洗衣机中的水量y(升)与时间x(分钟)之间的关系如下表所示:
| x | 0 | 2 | 4 | 16 | 16.5 | 17 | 18 | … |
| y | 0 | 20 | 40 | 40 | 29.5 | 20 | 2 | … |
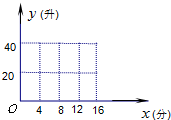
(1)试写出当x∈[0,16]时y关于x的函数解析式,并画出该函数的图象;
(2)根据排水阶段的2分钟点(x,y)的分布情况,可选用
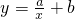 或y=c(x-20)2+d(其中a、b、c、d为常数),作为在排水阶段的2分钟内水量y与时间x之间关系的模拟函数.试分别求出这两个函数的解析式;
或y=c(x-20)2+d(其中a、b、c、d为常数),作为在排水阶段的2分钟内水量y与时间x之间关系的模拟函数.试分别求出这两个函数的解析式;(3)请问(2)中求出的两个函数哪一个更接近实际情况?(写出必要的步骤) 查看习题详情和答案>>
(文)某种洗衣机洗涤衣服时,需经过进水、清洗、排水、脱水四个连续的过程.假设进水时水量匀速增加,清洗时水量保持不变.已知进水时间为4分钟,清洗时间为12分钟,排水时间为2分钟,脱水时间为2分钟.洗衣机中的水量y(升)与时间x(分钟)之间的关系如下表所示:
请根据表中提供的信息解答下列问题:
(1)试写出当x∈[0,16]时y关于x的函数解析式,并画出该函数的图象;
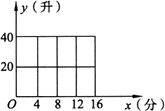
(2)根据排水阶段的2分钟点(x,y)的分布情况,可选用![]() 或y=c(x-20)2+d(其中a、b、c、d为常数),作为在排水阶段的2分钟内水量y与时间x之间关系的模拟函数.试分别求出这两个函数的解析式.
或y=c(x-20)2+d(其中a、b、c、d为常数),作为在排水阶段的2分钟内水量y与时间x之间关系的模拟函数.试分别求出这两个函数的解析式.
 (2006•静安区二模)某种洗衣机在洗涤衣服时,需经过进水、清洗、排水、脱水四个连续的过程.假设进水时水量匀速增加,清洗时水量保持不变.已知进水时间为4分钟,清洗时间为12分钟,排水时间为2分钟,脱水时间为2分钟.洗衣机中的水量y(升)与时间x(分钟)之间的关系如下表所示:
(2006•静安区二模)某种洗衣机在洗涤衣服时,需经过进水、清洗、排水、脱水四个连续的过程.假设进水时水量匀速增加,清洗时水量保持不变.已知进水时间为4分钟,清洗时间为12分钟,排水时间为2分钟,脱水时间为2分钟.洗衣机中的水量y(升)与时间x(分钟)之间的关系如下表所示:| x | 0 | 2 | 4 | 16 | 16.5 | 17 | 18 | … |
| y | 0 | 20 | 40 | 40 | 29.5 | 20 | 2 | … |
(1)试写出当x∈[0,16]时y关于x的函数解析式,并画出该函数的图象;
(2)根据排水阶段的2分钟点(x,y)的分布情况,可选用y=
| a |
| x |
(3)请问(2)中求出的两个函数哪一个更接近实际情况?(写出必要的步骤)