摘要：3．已知向量m=(1,1).向量与向量夹角为.且·=-1. (1)求向量, (2)若向量与向量=(1,0)的夹角为.向量=(cosA,2cos2).其中A.C为DABC的内角.且A.B.C依次成等差数列.试求|+|的取值范围. 解:(1)设=(x,y) 则由<,>=得:cos<,>== ① 由·=-1得x+y=-1 ② 联立①②两式得或 ∴= (2) ∵<,>= 得·=0 若=(1,0)则·=-1¹0 故¹ ∴= ∵2B=A+C.A+B+C=p ÞB= ∴C= +=(cosA,2cos2) = ∴|+|=== = = = = ∵0<A< ∴0<2A< ∴-1<cos(2A+)< ∴|+|Î()
网址：http://m.1010jiajiao.com/timu3_id_514982[举报]
已知常数m＞0，向量
=（0，1），向量
=（m，0），经过点A（m，0），以λ
+
为方向向量的直线与经过点B（-m，0），以λ
-4
为方向向量的直线交于点P，其中λ∈R．
（1）求点P的轨迹E；
（2）若m=2
，F（4，0），问是否存在实数k使得以Q（k，0）为圆心，|QF|为半径的圆与轨迹E在x轴上方交于M、N两点，并且|MF|+|NF|=3
．若存在求出k的值；若不存在，试说明理由．
查看习题详情和答案>>
| a |
| b |
| a |
| b |
| b |
| a |
（1）求点P的轨迹E；
（2）若m=2
| 5 |
| 5 |
（本题满分14分）
已知函数f(x)=sin(2x-
)-1, 设△ABC的内角A、B、C的对边长分别为a、b、c，且c=
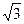,f(C)=0,若向量m=(1,sinA)与向量n=(2,sinB)共线，求a，b
（本题满分14分）
已知函数f(x)=sin(2x-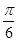
)-1,
设△ABC的内角A、B、C的对边长分别为a、b、c，且c=
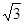,f(C)=0,若向量m=(1,sinA)与向量n=(2,sinB)共线，求a，b
查看习题详情和答案>>
, 设△ABC的内角A、B、C的对边长分别为a、b、c，且c=
,f(C)=0,若向量m=(1,sinA)与向量n=(2,sinB)共线，求a，b
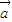=（0，1），向量
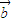=（m，0），经过点A（m，0），以
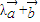为方向向量的直线与经过点B（-m，0），以
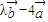为方向向量的直线交于点P，其中λ∈R．
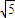，F（4，0），问是否存在实数k使得以Q（k，0）为圆心，|QF|为半径的圆与轨迹E在x轴上方交于M、N两点，并且|MF|+|NF|=3
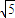．若存在求出k的值；若不存在，试说明理由．