题目内容
已知常数m>0,向量| a |
| b |
| a |
| b |
| b |
| a |
(1)求点P的轨迹E;
(2)若m=2
| 5 |
| 5 |
分析:(1)由λ
+
=(m,λ),知直线AP方程为y=
(x-m).由λ
-4
=(λm,-4),知直线NP方程为y=-
(x+m);所以
+
=1,由此结合m的取值情况能够求出点P的轨迹E.
(2)假设存在实数k满足要求,此时有圆Q:(x-k)2+y2=(4-k)2;椭圆E:
+
=1;其右焦点为F(4,0 ),且e=
.由圆Q与椭圆E的方程联立得2y2-5kx+20k-30=0,设M(x1,y1),N(x2,y2),则x1+x2=
k.△=25k2-4×2(20k-30),由此能求出存在实数k=1满足要求.
| a |
| b |
| λ |
| m |
| b |
| a |
| 4 |
| λm |
| x2 |
| m2 |
| y2 |
| 4 |
(2)假设存在实数k满足要求,此时有圆Q:(x-k)2+y2=(4-k)2;椭圆E:
| x2 |
| 20 |
| y2 |
| 4 |
| 2 |
| 5 |
| 5 |
| 5 |
| 2 |
解答:解:(1)∵λ
+
=( m,λ),
∴直线AP方程为y=
(x-m) ①
又λ
-4
=(λm,-4),∴直线NP方程为y=-
(x+m) ②
由①、②消去λ得 y2=-
(x2- m2 ),即
+
=1.
故当m=2时,轨迹E是以(0,0)为圆心,以2为半径的圆:x2+y2=4;
当m>2时,轨迹E是以原点为中心,以(±
,0)为焦点的椭圆:
当0<m<2时,轨迹E是以中心为原点,焦点为(0,±
)的椭圆.
(2)假设存在实数k满足要求,此时有圆Q:(x-k)2+y2=(4-k)2;
椭圆E:
+
=1;其右焦点为F(4,0 ),且e=
.
由圆Q与椭圆E的方程联立得2y2-5kx+20k-30=0,
设M(x1,y1),N(x2,y2),则x1+x2=
k ③
△=25k2-4×2(20k-30),
又|MF|=2
-
x1,|NF|=2
-
x2,而|MF|+|NF|=3
;
∴2
-
x1+2
-
x2=3
,
由此可得x1+x2=
④
由③、④得k=1,且此时△>0.故存在实数k=1满足要求.
| a |
| b |
∴直线AP方程为y=
| λ |
| m |
又λ
| b |
| a |
| 4 |
| λm |
由①、②消去λ得 y2=-
| 4 |
| m2 |
| x2 |
| m2 |
| y2 |
| 4 |
故当m=2时,轨迹E是以(0,0)为圆心,以2为半径的圆:x2+y2=4;
当m>2时,轨迹E是以原点为中心,以(±
| m2-4 |
当0<m<2时,轨迹E是以中心为原点,焦点为(0,±
| 4-m2 |
(2)假设存在实数k满足要求,此时有圆Q:(x-k)2+y2=(4-k)2;
椭圆E:
| x2 |
| 20 |
| y2 |
| 4 |
| 2 |
| 5 |
| 5 |
由圆Q与椭圆E的方程联立得2y2-5kx+20k-30=0,
设M(x1,y1),N(x2,y2),则x1+x2=
| 5 |
| 2 |
△=25k2-4×2(20k-30),
又|MF|=2
| 5 |
| 2 |
| 5 |
| 5 |
| 5 |
| 2 |
| 5 |
| 5 |
| 5 |
∴2
| 5 |
| 2 |
| 5 |
| 5 |
| 5 |
| 2 |
| 5 |
| 5 |
| 5 |
由此可得x1+x2=
| 5 |
| 2 |
由③、④得k=1,且此时△>0.故存在实数k=1满足要求.
点评:本题考查轨迹方程的求法和判断k是否存在.解题时要注意分类讨论思想和圆锥曲线性质的灵活运用.

练习册系列答案
 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目
 =(0,1),向量
=(0,1),向量 =(m,0),经过点A(m,0),以
=(m,0),经过点A(m,0),以 为方向向量的直线与经过点B(-m,0),以
为方向向量的直线与经过点B(-m,0),以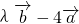 为方向向量的直线交于点P,其中λ∈R.
为方向向量的直线交于点P,其中λ∈R. ,F(4,0),问是否存在实数k使得以Q(k,0)为圆心,|QF|为半径的圆与轨迹E在x轴上方交于M、N两点,并且|MF|+|NF|=3
,F(4,0),问是否存在实数k使得以Q(k,0)为圆心,|QF|为半径的圆与轨迹E在x轴上方交于M、N两点,并且|MF|+|NF|=3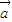 =(0,1),向量
=(0,1),向量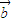 =(m,0),经过点A(m,0),以
=(m,0),经过点A(m,0),以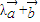 为方向向量的直线与经过点B(-m,0),以
为方向向量的直线与经过点B(-m,0),以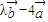 为方向向量的直线交于点P,其中λ∈R.
为方向向量的直线交于点P,其中λ∈R.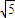 ,F(4,0),问是否存在实数k使得以Q(k,0)为圆心,|QF|为半径的圆与轨迹E在x轴上方交于M、N两点,并且|MF|+|NF|=3
,F(4,0),问是否存在实数k使得以Q(k,0)为圆心,|QF|为半径的圆与轨迹E在x轴上方交于M、N两点,并且|MF|+|NF|=3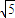 .若存在求出k的值;若不存在,试说明理由.
.若存在求出k的值;若不存在,试说明理由.