摘要：3．如图.在长方体ABCD-A1B1C1D1中.AB=5.AD=8.AA1=4.M为B1C1上一点.且B1M=2.点N在线段A1D上.A1D⊥AN.求: (1) , (2) 直线AD与平面ANM所成的角的大小, (3) 平面ANM与平面ABCD所成角的大小. 解:(1) 以A为原点.AB.AD.AA1所在直线 为x轴.y轴.z轴. 则D.A1 ) ∵ ∴ 知A1D⊥AM.又由已知A1D⊥AN.平面AMN.垂足为N. 因此AD与平面所成的角即是 易知 (3) ∵平面ABCD.A1N平面AMN. ∴分别成为平面ABCD和平面AMN的法向量. 设平面AMN与平面ABCD所成的角为.则
网址：http://m.1010jiajiao.com/timu3_id_514827[举报]
（2013•崇明县一模）如图，在长方体ABCD-A1B1C1D1中，AA1=AD=1，E为CD中点．（1）求证：B1E⊥AD1；
（2）若AB=2，求二面角A-B1E-A1的大小．
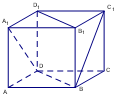如图，在长方体ABCD-A1B1C1D1中，AB=BC=2，A1D与BC1所成角为90°，则直线BC1与平面BB1D1D所成角的大小为
如图，在长方体ABCD-A1B1C1D1中，AD=AA1，AB=2，点E在棱AB上移动．（1）证明：D1E⊥A1D；
（2）AE等于何值时，平面D1DE⊥平面D1CE，并证明你的结论．
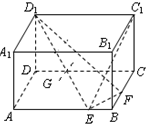如图，在长方体ABCD-A1B1C1D1中，已知AB=4，AD=3，AA1=2，E，F分别是棱AB，BC上的点，且EB=FB=1．
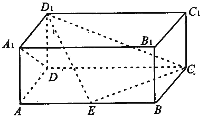如图，在长方体ABCD-A1B1C1D1中，AD=AA1=1，AB=2，点E在棱AB上移动．