摘要：B?分两类:(1)返回两人来自同一科室.返回有A种.故有C·A=6,(2)两人来自不同的科室.返回有2+1=3,故有(CC)·3=36种.共有42种.
网址：http://m.1010jiajiao.com/timu3_id_514458[举报]
已知椭圆C：
+
=1 (a＞b＞0)的离心率为e=
，以原点为圆心，椭圆短半轴长为半径的圆与直线x-y+2=0相切，A，B分别是椭圆的左右两个顶点，P为椭圆C上的动点．
（Ⅰ）求椭圆的标准方程；
（Ⅱ）若P与A，B均不重合，设直线PA与PB的斜率分别为k1，k2，证明：k1•k2为定值．
查看习题详情和答案>>
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 3 |
（Ⅰ）求椭圆的标准方程；
（Ⅱ）若P与A，B均不重合，设直线PA与PB的斜率分别为k1，k2，证明：k1•k2为定值．
已知椭圆C：
+
=1 (a＞b＞0)的离心率为e=
，以原点为圆心，椭圆短半轴长为半径的圆与直线x-y+2=0相切，A，B分别是椭圆的左右两个顶点，P为椭圆C上的动点．
（Ⅰ）求椭圆的标准方程；
（Ⅱ）若P与A，B均不重合，设直线PA与PB的斜率分别为k1，k2，证明：k1•k2为定值；
（Ⅲ）M为过P且垂直于x轴的直线上的点，若
=λ，求点M的轨迹方程，并说明轨迹是什么曲线．
查看习题详情和答案>>
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 3 |
（Ⅰ）求椭圆的标准方程；
（Ⅱ）若P与A，B均不重合，设直线PA与PB的斜率分别为k1，k2，证明：k1•k2为定值；
（Ⅲ）M为过P且垂直于x轴的直线上的点，若
| |OP| |
| |OM| |
（2012•自贡三模）己知椭圆C：
+
=1（a＞b＞0）的离心率为e=
，以原点为圆心，椭圆短半轴长为半径的圆与直线x-y+2=0相切，A，B分别是椭圆的左右两个顶点，P为椭圆C上的动点．
（I）求椭圆的标准方程；
（II） M为过P且垂直于x轴的直线上的点，若
=λ，求点M的轨迹方程，并说明轨迹是什么曲线．
查看习题详情和答案>>
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 3 |
（I）求椭圆的标准方程；
（II） M为过P且垂直于x轴的直线上的点，若
| |OP| |
| |OM| |
的左右两个焦点，O为坐标原点，点P 
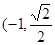）在椭圆上，线段PB与y轴的交点M为线段PB的中点。
是椭圆上异于长轴端点的任一点，对于△ABC，求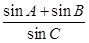
的值。
的离心率为
，以原点为圆心，椭圆短半轴长为半径的圆与直线x-y + 2 = 0相切,A,B分别是椭圆的左右两个顶点，P为椭圆C上的动点.
，求点M的轨迹方程，