摘要:掌握求动点的轨迹方程时常见的基本方法. [教学目标]
网址:http://m.1010jiajiao.com/timu3_id_513169[举报]
(2012•浙江模拟)平面内与直线平行的非零向量称为直线的方向向量;与直线的方向向量垂直的非零向量称为直线的法向量.在平面直角坐标系中,利用求动点的轨迹方程的方法,可以求出过点A(2,1)且法向量为
=(-1,2)的直线(点法式)方程为-(x-2)+2(y-1)=0,化简后得x-2y=0.类比以上求法,在空间直角坐标系中,经过点A(2,1,3),且法向量为
=(-1,2,1)的平面(点法式)方程为
查看习题详情和答案>>
| n |
| n |
x-2y-z+3=0
x-2y-z+3=0
(请写出化简后的结果).设圆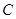 的极坐标方程为
的极坐标方程为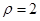 ,以极点为直角坐标系的原点,极轴为
,以极点为直角坐标系的原点,极轴为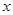 轴正半轴,两坐标系长度单位一致,建立平面直角坐标系.过圆
轴正半轴,两坐标系长度单位一致,建立平面直角坐标系.过圆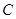 上的一点
上的一点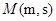 作平行于
作平行于 轴的直线
轴的直线 ,设
,设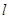 与
与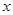 轴交于点
轴交于点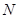 ,向量
,向量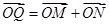 .
.
(Ⅰ)求动点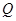 的轨迹方程;
的轨迹方程;
(Ⅱ)设点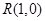 ,求
,求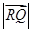 的最小值.
的最小值.
 ,
,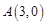 ,动点
,动点 到定点
到定点 距离与到定点
距离与到定点 的距离的比值是
的距离的比值是 .
. 时,记动点
时,记动点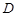 .
. 是圆
是圆 上任意一点,过
上任意一点,过 ,求
,求 的取值范围;
的取值范围; ,
, 是曲线
是曲线 ,有
,有 .试问无论
.试问无论 能恒和一个定圆相切吗?若能,求出这个定圆的方程;若不能,请说明理由.
能恒和一个定圆相切吗?若能,求出这个定圆的方程;若不能,请说明理由. 中,动点
中,动点 到两圆
到两圆 的圆心
的圆心 和
和 的距离的和等于
的距离的和等于 .
. 轴正半轴的交点C为直角顶点作此轨迹的内接等腰直角三角形ABC,试问:这样的等腰直角三角形是否存在?若存在,有几个?若不存在,请说明理由.
轴正半轴的交点C为直角顶点作此轨迹的内接等腰直角三角形ABC,试问:这样的等腰直角三角形是否存在?若存在,有几个?若不存在,请说明理由.