摘要：抛物线关于直线:对称的曲线方程是 ． 例题讲解 例1.过点任作一直线交轴于点A.过点作的垂线交轴于点B.点M分有向线段所成的比AM:MB=2:1.求点M的轨迹方程． 例2.过抛物线的顶点作互相垂直的两弦OA和OB (1)求AB中点P的轨迹方程, (2)求抛物线顶点O在AB上射影M的轨迹方程． 例3.自抛物线上任意一点P向其准线引垂线.垂足为Q.F为焦点.OP与FQ相交于点R.求点R的轨迹方程． 例4.设..为直角坐标平面内.轴正方向上的单位向量.若向量.且． (1)求点的轨迹C的方程, 作直线与曲线C交于A.B两点.设.是否存在这样的直线.使得四边形OAPB是矩形?若存在.求出直线的方程,若不存在.试说明理由． 课后作业 班级 学号 姓名
网址：http://m.1010jiajiao.com/timu3_id_512506[举报]
将抛物线C：x2=-4y上每一点的横坐标变为原来的
，纵坐标变为原来的3倍，得到曲线M．
（1）求曲线M的方程；
（2）直线l过点（3，0），若曲线C上存在两点关于直线l对称，求直线l的斜率的取值范围．
查看习题详情和答案>>
，纵坐标变为原来的3倍，得到曲线M．（1）求曲线M的方程；
（2）直线l过点（3，0），若曲线C上存在两点关于直线l对称，求直线l的斜率的取值范围．
查看习题详情和答案>>
双曲线M的中心在原点，并以椭圆
+
=1的焦点为焦点，以抛物线y2=-2
x的准线为右准线．
（Ⅰ）求双曲线M的方程；
（Ⅱ）设直线l：y=kx+3 与双曲线M相交于A、B两点，O是原点．
①当k为何值时，使得
•
=0？
②是否存在这样的实数k，使A、B两点关于直线y=mx+12对称？若存在，求出k的值；若不存在，说明理由．
查看习题详情和答案>>
| x2 |
| 25 |
| y2 |
| 13 |
| 3 |
（Ⅰ）求双曲线M的方程；
（Ⅱ）设直线l：y=kx+3 与双曲线M相交于A、B两点，O是原点．
①当k为何值时，使得
| OA |
| OB |
②是否存在这样的实数k，使A、B两点关于直线y=mx+12对称？若存在，求出k的值；若不存在，说明理由．
双曲线M的中心在原点，并以椭圆
的焦点为焦点，以抛物线
的准线为右准线.
（Ⅰ）求双曲线M的方程；
（Ⅱ）设直线
：
与双曲线M相交于A、B两点，O是原点.
① 当
为何值时，使得
?
② 是否存在这样的实数,使A、B两点关于直线
对称？若存在，求出的值；若不存在，说明理由.
的焦点为焦点，以抛物线
的准线为右准线.
：
与双曲线M相交于A、B两点，O是原点.
为何值时，使得
?
对称？若存在，求出
+
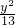=1的焦点为焦点，以抛物线y2=-2
x的准线为右准线．
•
=0？