题目内容
双曲线M的中心在原点,并以椭圆![]() 的焦点为焦点,以抛物线
的焦点为焦点,以抛物线![]() 的准线为右准线.
的准线为右准线.
(Ⅰ)求双曲线M的方程;
(Ⅱ)设直线![]() :
:![]() 与双曲线M相交于A、B两点,O是原点.
与双曲线M相交于A、B两点,O是原点.
① 当![]() 为何值时,使得
为何值时,使得![]()
![]()
![]()
![]() ?
?
② 是否存在这样的实数![]() ,使A、B两点关于直线
,使A、B两点关于直线![]() 对称?若存在,求出
对称?若存在,求出![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
(Ⅰ)双曲线M的方程为![]() .
.
(Ⅱ)当![]() 时,使得
时,使得![]()
![]()
![]()
![]() .
.
②当![]() 时,存在实数
时,存在实数![]() ,使A、B两点关于直线
,使A、B两点关于直线![]() 对称
对称
解析:
(Ⅰ)易知,椭圆![]() 的半焦距为:
的半焦距为:![]() ,
,
又抛物线![]() 的准线为:
的准线为:![]() . ----------2分
. ----------2分
设双曲线M的方程为![]() ,依题意有
,依题意有![]() ,
,
故![]() ,又
,又![]() .
.
∴双曲线M的方程为![]() . ----------4分
. ----------4分
(Ⅱ)设直线![]() 与双曲线M的交点为
与双曲线M的交点为![]() 、
、![]() 两点
两点
联立方程组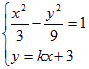 消去y得
消去y得 ![]() ,-------5分
,-------5分
∵![]() 、
、![]() 两点的横坐标是上述方程的两个不同实根, ∴
两点的横坐标是上述方程的两个不同实根, ∴![]()
∴![]()
![]() ,
,
从而有![]() ,
,![]() . ----------7分
. ----------7分
又![]() ,
,![]()
∴![]() .
.
若![]()
![]()
![]()
![]() ,则有
,则有 ![]() ,即
,即![]()
![]() .
.
∴当![]() 时,使得
时,使得![]()
![]()
![]()
![]() . ----------10分
. ----------10分
② 若存在实数![]() ,使A、B两点关于直线
,使A、B两点关于直线![]() 对称,则必有
对称,则必有 ![]() ,
,
因此,当m=0时,不存在满足条件的k;
当![]() 时,由
时,由 得
得 ![]()
![]()
![]()
![]()
∵A、B中点![]() 在直线
在直线![]() 上,
上,
∴![]() ,代入上式得
,代入上式得
![]() ,又
,又![]() , ∴
, ∴![]() ----------13分
----------13分
将![]() 代入并注意到
代入并注意到![]() ,得
,得 ![]() .
.
∴当![]() 时,存在实数
时,存在实数![]() ,使A、B两点关于直线
,使A、B两点关于直线![]() 对称----------14分
对称----------14分

练习册系列答案
相关题目
 +
+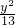 =1的焦点为焦点,以抛物线y2=-2
=1的焦点为焦点,以抛物线y2=-2 x的准线为右准线.
x的准线为右准线. •
• =0?
=0?