题目内容
双曲线M的中心在原点,并以椭圆 +
+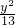 =1的焦点为焦点,以抛物线y2=-2
=1的焦点为焦点,以抛物线y2=-2 x的准线为右准线.
x的准线为右准线.
(Ⅰ)求双曲线M的方程;
(Ⅱ)设直线l:y=kx+3 与双曲线M相交于A、B两点,O是原点.
①当k为何值时,使得 •
• =0?
=0?
②是否存在这样的实数k,使A、B两点关于直线y=mx+12对称?若存在,求出k的值;若不存在,说明理由.
解:(Ⅰ)易知,椭圆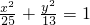 的半焦距为:
的半焦距为: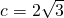 ,
,
又抛物线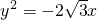 的准线为:x=
的准线为:x= .(2分)
.(2分)
设双曲线M的方程为 ,依题意有
,依题意有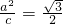
故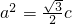
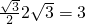 ,又b2=c2-a2=12-3=9.
,又b2=c2-a2=12-3=9.
∴双曲线M的方程为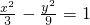 .(4分)
.(4分)
(Ⅱ)设直线l与双曲线M的交点为A(x1,y1)B(x2,y2)、两点
联立方程组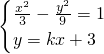 消去y得(k2-3)x2+6kx+18=0,(5分)
消去y得(k2-3)x2+6kx+18=0,(5分)
∵A(x1,y1)B(x2,y2)、两点的横坐标是上述方程的两个不同实根,∴k2-3≠0
∴△=36k2-4(k2-3)×18>0,解可得,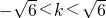 ,
,
从而有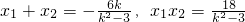 .(7分)
.(7分)
∴y1y2=(kx1+3)(kx2+3)=k2x1x2+3k(x1+x2)+9=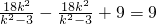 .
.
若 ,则有x1x2+y1y2=0,即
,则有x1x2+y1y2=0,即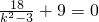
∴k=±1
∴当k=±1时,使得 ,(10分)
,(10分)
②若存在实k,使A、B两点关于直线y=mx+12对称,则必有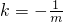
因此,当m=0时,不存在满足条件的k;
当m≠0时,由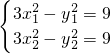 得3(x12-x22)-(y12-y22)=0
得3(x12-x22)-(y12-y22)=0
∴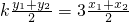
∵A、B中点P(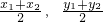 )在直线y=mx+12上,
)在直线y=mx+12上,
∴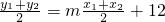 ,代入上式得
,代入上式得
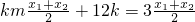 ,又km=-1,∴x1+x2=6k(13分)
,又km=-1,∴x1+x2=6k(13分)
将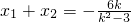 代入并注意到k≠0,得k=
代入并注意到k≠0,得k= .
.
∴当m≠0时,存在实数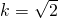 ,使A、B两点关于直线y=mx+12对称(14分)
,使A、B两点关于直线y=mx+12对称(14分)
分析:(Ⅰ)由题意可得所求的双曲线的半焦距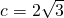 ,准线为:x=
,准线为:x= 从而可得
从而可得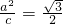 ,可求双曲线M的方程
,可求双曲线M的方程
(Ⅱ)①设直线l与双曲线M的交点为A(x1,y1)B(x2,y2)、联立方程组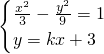 消去y(k2-3)x2+6kx+18=0,设A(x1,y1)B(x2,y2)、则k2-3≠0,△=36k2-4(k2-3)×18>0,解可得,
消去y(k2-3)x2+6kx+18=0,设A(x1,y1)B(x2,y2)、则k2-3≠0,△=36k2-4(k2-3)×18>0,解可得,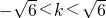 ,从而有
,从而有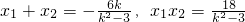
由 ,则有x1x2+y1y2=0,可求k
,则有x1x2+y1y2=0,可求k
②若存在实k,使A、B两点关于直线y=mx+12对称,则必有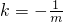
当m≠0时,利用点差法,由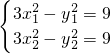 可得,3(x12-x22)-(y12-y22)=0即
可得,3(x12-x22)-(y12-y22)=0即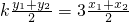 ,再由A、B中点P(
,再由A、B中点P(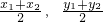 )在直线y=mx+12上,代入可求
)在直线y=mx+12上,代入可求
点评:本题主要考查了由双曲线的性质求解双曲线的方程及直线与曲线的位置关系,要求考生具备一定的逻辑推理与计算的能力,本题具有较大的综合性.
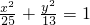 的半焦距为:
的半焦距为: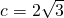 ,
,又抛物线
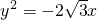 的准线为:x=
的准线为:x= .(2分)
.(2分)设双曲线M的方程为
 ,依题意有
,依题意有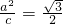
故
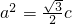
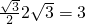 ,又b2=c2-a2=12-3=9.
,又b2=c2-a2=12-3=9.∴双曲线M的方程为
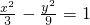 .(4分)
.(4分)(Ⅱ)设直线l与双曲线M的交点为A(x1,y1)B(x2,y2)、两点
联立方程组
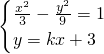 消去y得(k2-3)x2+6kx+18=0,(5分)
消去y得(k2-3)x2+6kx+18=0,(5分)∵A(x1,y1)B(x2,y2)、两点的横坐标是上述方程的两个不同实根,∴k2-3≠0
∴△=36k2-4(k2-3)×18>0,解可得,
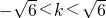 ,
,从而有
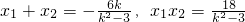 .(7分)
.(7分)∴y1y2=(kx1+3)(kx2+3)=k2x1x2+3k(x1+x2)+9=
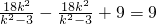 .
.若
 ,则有x1x2+y1y2=0,即
,则有x1x2+y1y2=0,即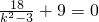
∴k=±1
∴当k=±1时,使得
 ,(10分)
,(10分)②若存在实k,使A、B两点关于直线y=mx+12对称,则必有
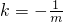
因此,当m=0时,不存在满足条件的k;
当m≠0时,由
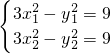 得3(x12-x22)-(y12-y22)=0
得3(x12-x22)-(y12-y22)=0∴
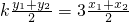
∵A、B中点P(
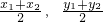 )在直线y=mx+12上,
)在直线y=mx+12上,∴
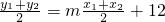 ,代入上式得
,代入上式得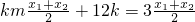 ,又km=-1,∴x1+x2=6k(13分)
,又km=-1,∴x1+x2=6k(13分)将
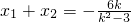 代入并注意到k≠0,得k=
代入并注意到k≠0,得k= .
.∴当m≠0时,存在实数
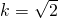 ,使A、B两点关于直线y=mx+12对称(14分)
,使A、B两点关于直线y=mx+12对称(14分)分析:(Ⅰ)由题意可得所求的双曲线的半焦距
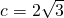 ,准线为:x=
,准线为:x= 从而可得
从而可得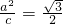 ,可求双曲线M的方程
,可求双曲线M的方程(Ⅱ)①设直线l与双曲线M的交点为A(x1,y1)B(x2,y2)、联立方程组
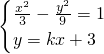 消去y(k2-3)x2+6kx+18=0,设A(x1,y1)B(x2,y2)、则k2-3≠0,△=36k2-4(k2-3)×18>0,解可得,
消去y(k2-3)x2+6kx+18=0,设A(x1,y1)B(x2,y2)、则k2-3≠0,△=36k2-4(k2-3)×18>0,解可得,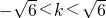 ,从而有
,从而有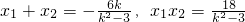
由
 ,则有x1x2+y1y2=0,可求k
,则有x1x2+y1y2=0,可求k②若存在实k,使A、B两点关于直线y=mx+12对称,则必有
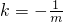
当m≠0时,利用点差法,由
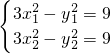 可得,3(x12-x22)-(y12-y22)=0即
可得,3(x12-x22)-(y12-y22)=0即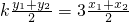 ,再由A、B中点P(
,再由A、B中点P(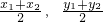 )在直线y=mx+12上,代入可求
)在直线y=mx+12上,代入可求点评:本题主要考查了由双曲线的性质求解双曲线的方程及直线与曲线的位置关系,要求考生具备一定的逻辑推理与计算的能力,本题具有较大的综合性.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目