摘要:会利用直线与圆锥曲线方程所组成的方程组消去一个变量.将交点问题(包括公共点个数.与交点坐标有关的问题)转化为一元二次方程根的问题.结合根与系数关系及判别式解决问题,
网址:http://m.1010jiajiao.com/timu3_id_512445[举报]
设点 为平面直角坐标系
为平面直角坐标系 中的一个动点(其中O为坐标原点),点P到定点
中的一个动点(其中O为坐标原点),点P到定点 的距离比点P到
的距离比点P到 轴的距离大
轴的距离大 。
。
(1)求点P的轨迹方程。
(2)若直线 与点P的轨迹相交于A、B两点,且
与点P的轨迹相交于A、B两点,且 ,求
,求 的值。
的值。
(3)设点P的轨迹是曲线C,点 是曲线C上的一点,求以Q为切点的曲线C 的切线方程。
是曲线C上的一点,求以Q为切点的曲线C 的切线方程。
【解析】本试题主要考查了轨迹方程的求解,利用直接法设点表示轨迹方程,并能利用所求的轨迹进行直线与圆锥曲线位置关系的运用。以及导数的几何意义的运用的综合试题。
查看习题详情和答案>>
设点 为平面直角坐标系
为平面直角坐标系 中的一个动点(其中O为坐标原点),点P到定点
中的一个动点(其中O为坐标原点),点P到定点 的距离比点P到
的距离比点P到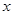 轴的距离大
轴的距离大 。
。
(1)求点P的轨迹方程。
(2)若直线 与点P的轨迹相交于A、B两点,且
与点P的轨迹相交于A、B两点,且 ,求
,求 的值。
的值。
(3)设点P的轨迹是曲线C,点 是曲线C上的一点,求以Q为切点的曲线C 的切线方程。
是曲线C上的一点,求以Q为切点的曲线C 的切线方程。
【解析】本试题主要考查了轨迹方程的求解,利用直接法设点表示轨迹方程,并能利用所求的轨迹进行直线与圆锥曲线位置关系的运用。以及导数的几何意义的运用的综合试题。
查看习题详情和答案>>
已知圆锥曲线C上任意一点到两定点F1(-1,0)、F2(1,0)的距离之和为常数,曲线C的离心率e=
.
(1)求圆锥曲线C的方程;
(2)设经过点F2的任意一条直线与圆锥曲线C相交于A、B,试证明在x轴上存在一个定点P,使
•
的值是常数.
查看习题详情和答案>>
| 1 |
| 2 |
(1)求圆锥曲线C的方程;
(2)设经过点F2的任意一条直线与圆锥曲线C相交于A、B,试证明在x轴上存在一个定点P,使
| PA |
| PB |
 中,圆锥曲线
中,圆锥曲线 的参数方程为
的参数方程为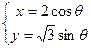 (
( 为参数),定点
为参数),定点 ,
, 是圆锥曲线
是圆锥曲线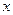 轴正半轴为极轴建立极坐标系,求经过点
轴正半轴为极轴建立极坐标系,求经过点 且平行于直线
且平行于直线 的直线
的直线 的极坐标方程;[来源:学科网ZXXK]
的极坐标方程;[来源:学科网ZXXK] 两点,求弦
两点,求弦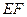 的长.
的长. 中,圆锥曲线
中,圆锥曲线 的参数方程为
的参数方程为 (
( 为参数),定点
为参数),定点 ,
, 是圆锥曲线
是圆锥曲线 轴正半轴为极轴建立极坐标系,求经过点
轴正半轴为极轴建立极坐标系,求经过点 且平行于直线
且平行于直线 的直线
的直线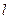 的极坐标方程;
的极坐标方程; 两点,求弦
两点,求弦 的长.
的长.