题目内容
已知圆锥曲线C上任意一点到两定点F1(-1,0)、F2(1,0)的距离之和为常数,曲线C的离心率e=| 1 |
| 2 |
(1)求圆锥曲线C的方程;
(2)设经过点F2的任意一条直线与圆锥曲线C相交于A、B,试证明在x轴上存在一个定点P,使
| PA |
| PB |
分析:(1)根据椭圆的定义判断出圆锥曲线C是椭圆,得到椭圆中的参数c的值,再根据离心率的公式求出参数a,利用三个参数的关系求出b,写出椭圆的方程.
(2)假设存在点p,分直线的斜率存在与不存在两种情况讨论,当斜率存在时,将直线的方程与椭圆的方程联立,利用韦达定理得到交点的坐标满足的关系,利用交点坐标表示出
•
,要使其为常数,令分子、分母的对应项的系数成比例,求出p的坐标,当直线的斜率不存在时将p的坐标代入检验即可.
(2)假设存在点p,分直线的斜率存在与不存在两种情况讨论,当斜率存在时,将直线的方程与椭圆的方程联立,利用韦达定理得到交点的坐标满足的关系,利用交点坐标表示出
| PA |
| PB |
解答:解:(1)依题意,设曲线C的方程为
+
=1(a>b>0),
∴c=1,
∵e=
=
,
∴a=2,
∴b=
=
,
所求方程为
+
=1.
(2)当直线AB不与x轴垂直时,设其方程为y=k(x-1),
由
,
得(3+4k2)x2-8k2x+4(k2-3)=0,
从而xA+xB=
,xA•xB=
,
设P(t,0),则
•
=(xA-t)(xB-t)+yAyB=(k2+1)xAxB-(t+k2)(xA+xB)+(k2+t2)=
当
=
,
解得t=
此时对?k∈R,
•
=-
;
当AB⊥x轴时,直线AB的方程为x=1,
xA=xB=1,yA(yB)=±
,
对t=
,
•
=(xA-t)(xB-t)+yAyB=
-
=-
,
即存在x轴上的点P(
,0),使
•
的值为常数-
.
| x2 |
| a2 |
| y2 |
| b2 |
∴c=1,
∵e=
| c |
| a |
| 1 |
| 2 |
∴a=2,
∴b=
| a2-c2 |
| 3 |
所求方程为
| x2 |
| 4 |
| y2 |
| 3 |
(2)当直线AB不与x轴垂直时,设其方程为y=k(x-1),
由
|
得(3+4k2)x2-8k2x+4(k2-3)=0,
从而xA+xB=
| 8k2 |
| 3+4k2 |
| 4(k2-3) |
| 3+4k2 |
设P(t,0),则
| PA |
| PB |
| 3t2-12+(-5-8t+4t2)k2 |
| 3+4k2 |
当
| 3t2-12 |
| 3 |
| -5-8t+4t2 |
| 4 |
解得t=
| 11 |
| 8 |
此时对?k∈R,
| PA |
| PB |
| 135 |
| 64 |
当AB⊥x轴时,直线AB的方程为x=1,
xA=xB=1,yA(yB)=±
| 3 |
| 2 |
对t=
| 11 |
| 8 |
| PA |
| PB |
| 9 |
| 64 |
| 9 |
| 4 |
| 135 |
| 64 |
即存在x轴上的点P(
| 11 |
| 8 |
| PA |
| PB |
| 135 |
| 64 |
点评:求圆锥曲线的方程一般利用待定系数法,注意椭圆中三个参数a,b,c的关系满足a2=b2+c2;解决直线与圆锥曲线的关系问题,一般是将直线的方程与圆锥曲线的方程联立得到二次方程,利用韦达定理找突破口.

练习册系列答案
相关题目
 .
. 的值是常数.
的值是常数.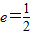 .
.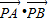 的值是常数.
的值是常数.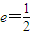 .
.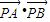 的值是常数.
的值是常数.