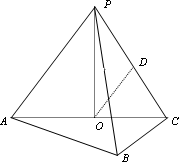
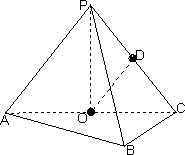
摘要：如图.在三棱锥P-ABC中.AB⊥BC.AB=BC=PA.点O.D分别是AC.PC的中点.OP⊥底面ABC. (1)求证:OD∥平面PAB, (2)求直线OD与平面PBC所成角的大小． 高三数学教学案 第九章 立体几何 第十一课时 二面角(一) 考纲摘录 掌握平面与平面所成角的概念.能正确画出两个平面位置关系的图形.并能运用二面 角及其平面角的概念进行计算和证明． 知识概要
网址：http://m.1010jiajiao.com/timu3_id_512427[举报]
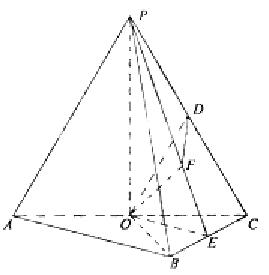
18．如图，在三棱锥P－ABC中，AB⊥BC，AB＝BC＝kPA，点O、D分别是AC、PC的中点，OP⊥底面ABC．
(Ⅰ)求证OD∥平面PAB；
(Ⅱ)当k＝
时，求直线PA与平面PBC所成角的大小；
(Ⅲ) 当k取何值时，O在平面PBC内的射影恰好为△PBC的重心？
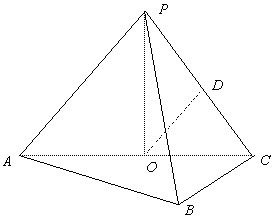
18.如图，在三棱锥P－ABC中，AB⊥BC，AB＝BC＝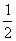
PA，点O、D分别是AC、PC的中点，OP⊥底面ABC.
PA，点O、D分别是AC、PC的中点，OP⊥底面ABC.(Ⅰ)求证：OD∥平面PAB；
(Ⅱ)求直线OD与平面PBC所成角的大小.
| |||||||||||
时，求直线PA与平面PBC所成角的大小；
时，求直线PA与平面PBC所成角的大小；