摘要： 已知函数在上有意义..且满足.时.有) (1)证明在上是奇函数; (2)对数列..求; 中的数列.求证: .
网址：http://m.1010jiajiao.com/timu3_id_511620[举报]
已知函数f（x）的定义域为R，若存在常数m＞0，对任意x∈R，有|f（x）|＜m|x|，则称f（x）为F函数．给出下列函数：
①f（x）=x2；
②f（x）=sinx+cosx；
③f(x)=
；
④f（x）是定义在R上的奇函数，且满足对一切实数x1，x2均有|f（x1）-f（x2）|≤2|x1-x2|．
其中是F函数的序号为（ ）
①f（x）=x2；
②f（x）=sinx+cosx；
③f(x)=
| x |
| x2+x+1 |
④f（x）是定义在R上的奇函数，且满足对一切实数x1，x2均有|f（x1）-f（x2）|≤2|x1-x2|．
其中是F函数的序号为（ ）
| A、②④ | B、①③ | C、③④ | D、①② |
已知函数f(x)在(-1，1)上有意义，f(
)=-1，且对任意的x、y∈（-1，1）都有f(x)+f(y)=f(
)．
（1）若数列{xn}满足x1=
，xn+1=
(n∈N*)，求f(xn)．
（2）求1+f(
)+f(
)…+f(
)+f(
)的值．
查看习题详情和答案>>
| 1 |
| 2 |
| x+y |
| 1+xy |
（1）若数列{xn}满足x1=
| 1 |
| 2 |
| 2xn | ||
1+
|
（2）求1+f(
| 1 |
| 5 |
| 1 |
| 11 |
| 1 |
| n2+3n+1 |
| 1 |
| n+2 |
已知函数f(x)在(-1，1)上有意义，f(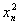
)=-1，且对任意的x、y∈(-1，1)都有f(x)+f(y)=(
)
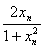)=-1，且对任意的x、y∈(-1，1)都有f(x)+f(y)=()(Ⅰ)判断函数f(x)的奇偶性；
(Ⅱ)若数列{xn}满足x1=
，xn+1=
(n∈N*)，求f(xn)；
(Ⅲ)求证：
(n∈N*)．
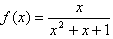；④f（x）是定义在R上的奇函数，且满足对一切实数x1，x2均有|f（x1）-f（x2）|≤2|x1-x2|。其中是F函数的序号为