题目内容
下面给出的四个命题中:①对任意的n∈N*,点Pn(n,an)都在直线y=2x+1上是数列an为等差数列的充分不必要条件;
②“m=-2”是直线(m+2)x+my+1=0与“直线(m-2)x+(m+2)y-3=0相互垂直”的必要不充分条件;
③设圆x2+y2+Dx+Ey+F=0(D2+E2-4F>0)与坐标轴有4个交点A(x1,0),B(x2,0),C(0,y1),D(0,y2),则有x1x2-y1y2=0;
④将函数y=cos2x的图象向右平移
| π |
| 3 |
| π |
| 6 |
其中是真命题的有
分析:利用等差数列通项公式的形式判断出①对;利用两直线垂直的充要条件判断出②不正确,利用韦达定理判断出③正确;利用图象的平移变换及三角函数的诱导公式判断出④正确.
解答:解:对于①,∵点Pn(n,an)都在直线y=2x+1上∴数列an为等差数列但反之不成立.故①对
对于②,∵直线(m+2)x+my+1=0与“直线(m-2)x+(m+2)y-3=0相互垂直的充要条件是
(m+2)(m-2)+m(m+2)=0即m=-2或m=1
所以②“m=-2”是直线(m+2)x+my+1=0与“直线(m-2)x+(m+2)y-3=0相互垂直”充分不必要条件;
故②不正确
对于③,令y=0得x2+Dx+F=0∴x1x2=-F同理y1y2=-F所以x1x2-y1y2=0,故③正确
对于④,将函数y=cos2x的图象向右平移
个单位,得到函数y=cos2(x-
)=sin(2x-
),故④正确
故答案为①③④
对于②,∵直线(m+2)x+my+1=0与“直线(m-2)x+(m+2)y-3=0相互垂直的充要条件是
(m+2)(m-2)+m(m+2)=0即m=-2或m=1
所以②“m=-2”是直线(m+2)x+my+1=0与“直线(m-2)x+(m+2)y-3=0相互垂直”充分不必要条件;
故②不正确
对于③,令y=0得x2+Dx+F=0∴x1x2=-F同理y1y2=-F所以x1x2-y1y2=0,故③正确
对于④,将函数y=cos2x的图象向右平移
| π |
| 3 |
| π |
| 3 |
| π |
| 6 |
故答案为①③④
点评:在解决图象的平移变换时,一定要注意左右平移的单位是自变量x本身上变换的值的绝对值.

练习册系列答案
相关题目
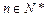 ,点
,点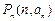 都在直线
都在直线 上是数列
上是数列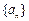 为等差数列的充分不必要条件;
为等差数列的充分不必要条件;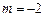 ”是直线
”是直线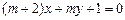 与“直线
与“直线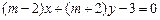 相互垂直”的必要不充分条件;
相互垂直”的必要不充分条件;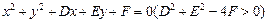 与坐标轴有4个交点
与坐标轴有4个交点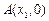 ,
,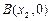 ,
,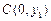 ,
,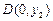 ,则有
,则有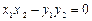 ;
;
 ,点
,点 都在直线
都在直线 上是数列
上是数列 为等差数列的充分不必要条件;
为等差数列的充分不必要条件; ”是直线
”是直线 与“直线
与“直线 相互垂直”的必要不充分条件;
相互垂直”的必要不充分条件; 与坐标轴有4个交点
与坐标轴有4个交点 ,
, ,
, ,
,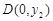 ,则有
,则有 ;
;