题目内容
关于数列有下列四个判断:
①若a,b,c,d成等比数列,则a+b,b+c,c+d也成等比数列;
②若数列{an}是等比数列,则Sn,S2n-Sn,S3n-S2n…也成等比数列;
③若数列{an}既是等差数列也是等比数列,则{an}为常数列;
④数列{an}的前n项的和为Sn,且Sn=an-1(a∈R),则{an}为等差或等比数列;
⑤数列{an}为等差数列,且公差不为零,则数列{an}中不会有am=an(m≠n).
其中正确命题的序号是
①若a,b,c,d成等比数列,则a+b,b+c,c+d也成等比数列;
②若数列{an}是等比数列,则Sn,S2n-Sn,S3n-S2n…也成等比数列;
③若数列{an}既是等差数列也是等比数列,则{an}为常数列;
④数列{an}的前n项的和为Sn,且Sn=an-1(a∈R),则{an}为等差或等比数列;
⑤数列{an}为等差数列,且公差不为零,则数列{an}中不会有am=an(m≠n).
其中正确命题的序号是
②③④⑤
②③④⑤
.(请将正确命题的序号都填上)分析:①1,-1,1,-1成等比数列,但1-1,-1+1,1-1不成等比数列;
②根据等比数列前n项和的性质,可知结论正确;
③数列{an}是等比数列,所以an=a1qn-1,an+1=a1qn,从而an+1-an=a1qn-1(q-1),根据若数列{an}是等差数列,即可得到{an}为常数列;
④数列{an}的前n项的和为Sn,且Sn=an-1(a∈R),则n≥2时,an=Sn-Sn-1 =(a-1)an-1,当n=1时,结论也成立.当a=0时,{an}为等差数列;当a≠0时,{an}为等比数列;
⑤数列{an}为等差数列,所以am-an=(m-n)d,根据公差不为零,m≠n,可得am≠an.
②根据等比数列前n项和的性质,可知结论正确;
③数列{an}是等比数列,所以an=a1qn-1,an+1=a1qn,从而an+1-an=a1qn-1(q-1),根据若数列{an}是等差数列,即可得到{an}为常数列;
④数列{an}的前n项的和为Sn,且Sn=an-1(a∈R),则n≥2时,an=Sn-Sn-1 =(a-1)an-1,当n=1时,结论也成立.当a=0时,{an}为等差数列;当a≠0时,{an}为等比数列;
⑤数列{an}为等差数列,所以am-an=(m-n)d,根据公差不为零,m≠n,可得am≠an.
解答:解:①1,-1,1,-1成等比数列,但1-1,-1+1,1-1不成等比数列,所以①不正确;
②根据等比数列前n项和的性质,可知若数列{an}是等比数列,则Sn,S2n-Sn,S3n-S2n…也成等比数列,所以②正确;
③数列{an}是等比数列,所以an=a1qn-1,an+1=a1qn,∴an+1-an=a1qn-1(q-1)
∵若数列{an}是等差数列,∴q=1,∴{an}为常数列,∴③正确;
④数列{an}的前n项的和为Sn,且Sn=an-1(a∈R),则n≥2时,an=Sn-Sn-1 =(a-1)an-1,当n=1时,结论也成立.当a=0时,{an}为等差数列;当a≠0时,{an}为等比数列,所以④正确;
⑤数列{an}为等差数列,∴am-an=(m-n)d,∵公差不为零,m≠n,∴am≠an.所以⑤正确
所以正确的命题序号为②③④⑤
故答案为:②③④⑤
②根据等比数列前n项和的性质,可知若数列{an}是等比数列,则Sn,S2n-Sn,S3n-S2n…也成等比数列,所以②正确;
③数列{an}是等比数列,所以an=a1qn-1,an+1=a1qn,∴an+1-an=a1qn-1(q-1)
∵若数列{an}是等差数列,∴q=1,∴{an}为常数列,∴③正确;
④数列{an}的前n项的和为Sn,且Sn=an-1(a∈R),则n≥2时,an=Sn-Sn-1 =(a-1)an-1,当n=1时,结论也成立.当a=0时,{an}为等差数列;当a≠0时,{an}为等比数列,所以④正确;
⑤数列{an}为等差数列,∴am-an=(m-n)d,∵公差不为零,m≠n,∴am≠an.所以⑤正确
所以正确的命题序号为②③④⑤
故答案为:②③④⑤
点评:本题以命题为载体,考查数列的性质,解题时需要谨慎思考,一一判断.

练习册系列答案
相关题目
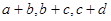 也成等比数列;
也成等比数列;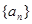 既是等差数列,也是等比数列,则
既是等差数列,也是等比数列,则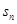 ,且
,且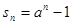 ,(a
,(a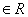 ),则
),则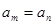
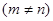
 ,则{an}为等差或等比数列;
,则{an}为等差或等比数列;