摘要：动直线与抛物线相交于A.B两点.M是AB的中点.若M始终落在曲线上.求证:直线过定点． 高三数学教学案 第八章 圆锥曲线 第十四课时 解析几何综合应用 考纲摘录 掌握解析几何的一些综合应用． 例题讲解 例1.双曲线C:.若C的上半支的顶点为A.且与直线交于点P.以A为焦点.M(0.m)为顶点的开口向下的抛物线通过P.当C的一条渐近线的斜率在区间上变化时.求直线PM斜率的最大值． 例2.抛物线及定点.M是抛物线上的点.设直线AM.BM与抛物线的另一交点分别为M1.M2． 求证:当点M在抛物线上变动时(只要M1.M2存在且M1.M2是不同的两点).直线M1.M2恒过一定点.并求定点坐标． 例3.椭圆的焦点在轴上.A是它的右顶点.这个椭圆与射线的交点是B.以A为焦点.过点B且开口向左的抛物线顶点是(m.0).当椭圆离心率时.求:m的范围． 例4.△的面积是S.且 (1)若.求:向量与的夹角的范围, (2)设.若以O为中心.F为焦点的椭圆.经过点.求:的纵坐标, 的条件下.当取得最小值时.求:此椭圆的方程． 课后作业 班级 学号 姓名
网址：http://m.1010jiajiao.com/timu3_id_511159[举报]
（9分）已知动直线
与抛物线
相交于A点，动点B的坐标是
（Ⅰ）求线段AB的中点M的轨迹
的方程；
（Ⅱ）若过点N（1，0）的直线
交轨迹于
、
两点，点
是坐标原点，若
面积为4，求直线的倾斜角
.
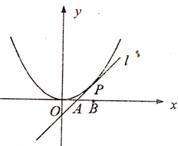
抛物线
在点P处的切线
分别交x轴、y轴于不同的两点A、B，
。当点P在C上移动时，点M的轨迹为D。
（1）求曲线D的方程：
（2）圆心E在y轴上的圆与直线相切于点P，当|PE|=|PA|，求圆的方程。
查看习题详情和答案>>
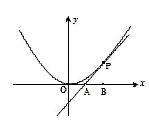
抛物线
在点P处的切线
分别交x轴、y轴于不同的两点A、B，
。当点P在C上移动时，点M的轨迹为D。
（1）求曲线D的方程：
（2）圆心E在y轴上的圆与直线相切于点P，当|PE|=|PA|，求圆的方程。
在点P处的切线分别交x轴、y轴于不同的两点A、B，。当点P在C上移动时，点M的轨迹为D。（1）求曲线D的方程：
（2）圆心E在y轴上的圆与直线
相切于点P，当|PE|=|PA|，求圆的方程。
与抛物线
相切于点P（2，1），且与x轴交于点A，O为
，求动点M的轨迹C 的方程；
（斜率不等于零）与（1）中的轨迹C交于不同的两点E、F（E在B、F之间），且
，试求λ的取值范围。
与抛物线
相切于点P(2, 1)，且与
轴交于点A，定点B的坐标为(2, 0) . 
，求点M的轨迹C；
（斜率不等于零）与（I）中的轨迹C交于不同的两点E、F（E在B、F之间），试求
OBE与