摘要:求最大的实数.使得当实系数多项式的所有根都是非负实数时.只要≥min{三根}.就有≥.并且问上式中等号何时成立? 数学竞赛单元训练题 解析几何
网址:http://m.1010jiajiao.com/timu3_id_510914[举报]
| |||||||||||||||
当p1,p2,…,pn均为正数时,称
为p1,p2,…,pn的“均倒数”.已知数列{an}的各项均为正数,且其前n项的“均倒数”为
.
(1)求数列{an}的通项公式;
(2)设cn=
(n∈N*),试比较cn+1与cn的大小;
(3)设函数f(x)=-x2+4x-
,是否存在最大的实数λ,使当x≤λ时,对于一切正整数n,都有f(x)≤0恒成立?
查看习题详情和答案>>
| n |
| p1+p2+…+pn |
| 1 |
| 2n+1 |
(1)求数列{an}的通项公式;
(2)设cn=
| an |
| 2n+1 |
(3)设函数f(x)=-x2+4x-
| an |
| 2n+1 |
当p1,p2,…,pn均为正数时,称
为p1,p2,…,pn的“均倒数”.已知数列{an}的各项均为正数,且其前n项的“均倒数”为
.
(Ⅰ)试求数列{an}的通项公式;
(Ⅱ)设cn=
,试判断并说明cn+1-cn(n∈N*)的符号;
(Ⅲ)已知bn=tan(t>0),记数列{bn}的前n项和为Sn,试求
的值;
(Ⅳ)设函数f(x)=-x2+4x-
,是否存在最大的实数λ,使当x≤λ时,对于一切正整数n,都有f(x)≤0恒成立?
查看习题详情和答案>>
| n |
| p1+p2+…+pn |
| 1 |
| 2n+1 |
(Ⅰ)试求数列{an}的通项公式;
(Ⅱ)设cn=
| an |
| 2n+1 |
(Ⅲ)已知bn=tan(t>0),记数列{bn}的前n项和为Sn,试求
| Sn+1 |
| Sn |
(Ⅳ)设函数f(x)=-x2+4x-
| an |
| 2n+1 |
已知点P1(a1,b1),P2(a2,b2),…,Pn(an,bn)(n为正整数)都在函数y=(
)x的图象上,且数列{an} 是a1=1,公差为d的等差数列.
(1)证明:数列{bn} 是等比数列;
(2)若公差d=1,以点Pn的横、纵坐标为边长的矩形面积为cn,求最大的实数t,使cn≤
(t∈R,t≠0)对一切正整数n恒成立;
(3)对(2)中的数列{an},对每个正整数k,在ak与ak+1之间插入3k-1个3(如在a1与a2之间插入30个3,a2与a3之间插入31个3,a3与a4之间插入32个3,…,依此类推),得到一个新的数列{dn},设Sn是数列{dn}的前n项和,试探究2008是否为数列{Sn}中的某一项,写出你探究得到的结论并给出证明. 查看习题详情和答案>>
| 1 |
| 2 |
(1)证明:数列{bn} 是等比数列;
(2)若公差d=1,以点Pn的横、纵坐标为边长的矩形面积为cn,求最大的实数t,使cn≤
| 1 |
| t |
(3)对(2)中的数列{an},对每个正整数k,在ak与ak+1之间插入3k-1个3(如在a1与a2之间插入30个3,a2与a3之间插入31个3,a3与a4之间插入32个3,…,依此类推),得到一个新的数列{dn},设Sn是数列{dn}的前n项和,试探究2008是否为数列{Sn}中的某一项,写出你探究得到的结论并给出证明. 查看习题详情和答案>>
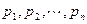 均为正数时,称
均为正数时,称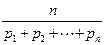 为
为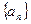 的各项均为正数,且其前
的各项均为正数,且其前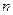 项的“均倒数”为
项的“均倒数”为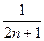 .
.
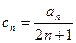
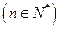 ,试比较
,试比较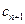 与
与 的大小;
的大小;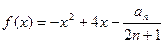 ,是否存在最大的实数
,是否存在最大的实数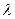 ,使当
,使当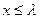
 时,对于一切正
时,对于一切正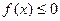 恒成立?
恒成立?