摘要：向量是数形结合的典范.向量的几何表示法--有向线段表示法是运用几何性质解决向量问题的基础.在向量的运算过程中.借助于图形性质不仅可以给抽象运算以直观解释.有时甚至更简捷. 向量运算中的基本图形:①向量加减法则:三角形或平行四边形,②实数与向量乘积的几何意义--共线,③定比分点基本图形--起点相同的三个向量终点共线等.
网址：http://m.1010jiajiao.com/timu3_id_510306[举报]
（2007•普陀区一模）现有问题：“对任意x＞0，不等式x-a+
＞0恒成立，求实数a的取值范围．”有两位同学用数形结合的方法分别提出了自己的解题思路和答案：
学生甲：在一个坐标系内作出函数f(x)=
和g（x）=-x+a的大致图象，随着a的变化，要求f（x）的图象再y轴右侧的部分恒在g（x）的上方．可解得a的取值范围是[0，+∞]
学生乙：在坐标平面内作出函数f(x)=x+a+
的大致图象，随着a的变化，要求f（x）的图象再y轴右侧的部分恒在直线y=2a的上方．可解得a的取值范围是[0，1]．
则以下对上述两位同学的解题方法和结论的判断都正确的是（ ）
| 1 |
| x+a |
学生甲：在一个坐标系内作出函数f(x)=
| 1 |
| x+a |
学生乙：在坐标平面内作出函数f(x)=x+a+
| 1 |
| x+a |
则以下对上述两位同学的解题方法和结论的判断都正确的是（ ）
查看习题详情和答案>>
现有问题：“对任意x＞0，不等式x-a+
＞0恒成立，求实数a的取值范围．”有两位同学用数形结合的方法分别提出了自己的解题思路和答案：
学生甲：在一个坐标系内作出函数
和g（x）=-x+a的大致图象，随着a的变化，要求f（x）的图象再y轴右侧的部分恒在g（x）的上方．可解得a的取值范围是[0，+∞]
学生乙：在坐标平面内作出函数
的大致图象，随着a的变化，要求f（x）的图象再y轴右侧的部分恒在直线y=2a的上方．可解得a的取值范围是[0，1]．
则以下对上述两位同学的解题方法和结论的判断都正确的是（ ）
A．甲同学方法正确，结论错误
B．乙同学方法正确，结论错误
C．甲同学方法正确，结论正确
D．乙同学方法错误，结论正确
查看习题详情和答案>>
＞0恒成立，求实数a的取值范围．”有两位同学用数形结合的方法分别提出了自己的解题思路和答案：学生甲：在一个坐标系内作出函数
和g（x）=-x+a的大致图象，随着a的变化，要求f（x）的图象再y轴右侧的部分恒在g（x）的上方．可解得a的取值范围是[0，+∞]学生乙：在坐标平面内作出函数
的大致图象，随着a的变化，要求f（x）的图象再y轴右侧的部分恒在直线y=2a的上方．可解得a的取值范围是[0，1]．则以下对上述两位同学的解题方法和结论的判断都正确的是（ ）
A．甲同学方法正确，结论错误
B．乙同学方法正确，结论错误
C．甲同学方法正确，结论正确
D．乙同学方法错误，结论正确
查看习题详情和答案>>
对对数函数的图象和性质的研究，教材是根据互为反函数的图象特征，由指数函数的图象再作出其关于直线y＝x的图象，即得对数函数的图象，在数形结合的数学思想指导下，推得对数函数的性质．请归纳对数函数y＝logax(a＞0且a≠1)的性质．
现有问题：“对任意x＞0，不等式x-a+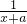
＞0恒成立，求实数a的取值范围．”有两位同学用数形结合的方法分别提出了自己的解题思路和答案：
学生甲：在一个坐标系内作出函数
和g（x）=-x+a的大致图象，随着a的变化，要求f（x）的图象再y轴右侧的部分恒在g（x）的上方．可解得a的取值范围是[0，+∞]
学生乙：在坐标平面内作出函数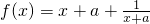
的大致图象，随着a的变化，要求f（x）的图象再y轴右侧的部分恒在直线y=2a的上方．可解得a的取值范围是[0，1]．
则以下对上述两位同学的解题方法和结论的判断都正确的是
- A.甲同学方法正确，结论错误
- B.乙同学方法正确，结论错误
- C.甲同学方法正确，结论正确
- D.乙同学方法错误，结论正确
（a>b>0）,点
在椭圆上。