摘要:二轮复习更应注重变式训练.拓展.举一反三.在激发学生学习兴趣的同时.增加了容量.拓展了学生的思维空间.由于时间紧.任务重.更要注意时间的有效利用.比如为减少课堂画图时间.我们可以用一个四面体为载体.解决一系列问题.包括特征图形.特殊几何体.共点.共线.共面问题.线面关系的判定问题.各种角与距离.面积与体积的计算问题.“割 与“补 的方法.一些重点结论的问题.如cosα=cosβcosγ.cosα=s' /s.l2=a2+b2+c2等等.以基本图形带动一系列知识的复习.达到系统复习内容.突出重点的目的.
网址:http://m.1010jiajiao.com/timu3_id_510027[举报]
(2009•卢湾区一模)在等差数列{an}中,公差为d,前n项和为Sn.在等比数列{bn}中,公比为q,前n项和为S'n(n∈N*).
(1)在等差数列{an}中,已知S10=30,S20=100,求S30.
(2)在等差数列{an}中,根据要求完成下列表格,并对①、②式加以证明(其中m、m1、m2、n∈N*).
(3)在下列各题中,任选一题进行解答,不必证明,解答正确得到相应的分数(若选做二题或更多题,则只批阅其中分值最高的一题,其余各题的解答,不管正确与否,一律视为无效,不予批阅):
(ⅰ) 类比(2)中①式,在等比数列{bn}中,写出相应的结论.
(ⅱ) (解答本题,最多得5分)类比(2)中②式,在等比数列{bn}中,写出相应的结论.
(ⅲ) (解答本题,最多得6分)在等差数列{an}中,将(2)中的①推广到一般情况.
(ⅳ) (解答本题,最多得6分)在等比数列{bn}中,将(2)中的①推广到一般情况.
查看习题详情和答案>>
(1)在等差数列{an}中,已知S10=30,S20=100,求S30.
(2)在等差数列{an}中,根据要求完成下列表格,并对①、②式加以证明(其中m、m1、m2、n∈N*).
| 用Sm表示S2m | S2m=2Sm+m2d | ||||
| 用Sm1、Sm2表示Sm1+m2 | Sm1+m2= Sm1+Sm2+m1m2d Sm1+Sm2+m1m2d ① | ||||
| 用Sm表示Snm | Snm= nSm+
nSm+ ②
|
(ⅰ) 类比(2)中①式,在等比数列{bn}中,写出相应的结论.
(ⅱ) (解答本题,最多得5分)类比(2)中②式,在等比数列{bn}中,写出相应的结论.
(ⅲ) (解答本题,最多得6分)在等差数列{an}中,将(2)中的①推广到一般情况.
(ⅳ) (解答本题,最多得6分)在等比数列{bn}中,将(2)中的①推广到一般情况.
在等差数列{an}中,公差为d,前n项和为Sn.在等比数列{bn}中,公比为q,前n项和为S'n(n∈N*).
(1)在等差数列{an}中,已知S10=30,S20=100,求S30.
(2)在等差数列{an}中,根据要求完成下列表格,并对①、②式加以证明(其中m、m1、m2、n∈N*).
(3)在下列各题中,任选一题进行解答,不必证明,解答正确得到相应的分数(若选做二题或更多题,则只批阅其中分值最高的一题,其余各题的解答,不管正确与否,一律视为无效,不予批阅):
(ⅰ) 类比(2)中①式,在等比数列{bn}中,写出相应的结论.
(ⅱ) (解答本题,最多得5分)类比(2)中②式,在等比数列{bn}中,写出相应的结论.
(ⅲ) (解答本题,最多得6分)在等差数列{an}中,将(2)中的①推广到一般情况.
(ⅳ) (解答本题,最多得6分)在等比数列{bn}中,将(2)中的①推广到一般情况.
查看习题详情和答案>>
(1)在等差数列{an}中,已知S10=30,S20=100,求S30.
(2)在等差数列{an}中,根据要求完成下列表格,并对①、②式加以证明(其中m、m1、m2、n∈N*).
| 用Sm表示S2m | S2m=2Sm+m2d |
用 、 、 表示 表示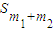 |  =______① =______① |
| 用Sm表示Snm | Snm=______② |
(ⅰ) 类比(2)中①式,在等比数列{bn}中,写出相应的结论.
(ⅱ) (解答本题,最多得5分)类比(2)中②式,在等比数列{bn}中,写出相应的结论.
(ⅲ) (解答本题,最多得6分)在等差数列{an}中,将(2)中的①推广到一般情况.
(ⅳ) (解答本题,最多得6分)在等比数列{bn}中,将(2)中的①推广到一般情况.
查看习题详情和答案>>