摘要：18．正三棱柱ABC-A1B1C1的侧棱长和底面边长都等于2.D是BC上一点.且AD⊥BC. ⑴求证:A1B∥平面ADC1; ⑵求截面ADC1与侧面ACC1A1所成的二面角D-AC1-C的大小. 19．如图.某建筑物的基本单元可近似地按以下方法构作:先在地平面内作菱形ABCD.其边长为1.∠BAD＝60°.再在平面的上侧.分别以△ABD与△CBD为底面安装上相同的正三棱锥P-ABD与Q-CBD.∠APB＝90°. ⑴求证:PQ⊥BD, ⑵求二面角P-BD-Q的大小, ⑶求点P到平面QBD的距离.
网址：http://m.1010jiajiao.com/timu3_id_509577[举报]
(本小题满分12分)
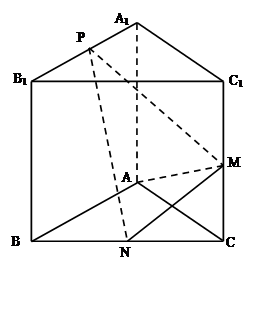
如图，已知三棱柱ABC-A1B1C1的侧棱与底面垂直，AA1=AB=AC=1,且AB⊥AC，M是CC1的中点，N是BC的中点，点P在直线A1B1上，且满足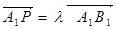
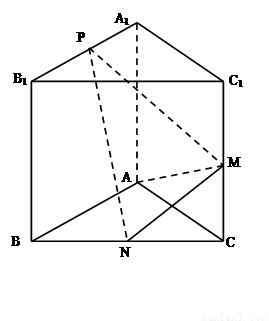
(1)证明：PN⊥AM
(2)若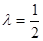
，求直线AA1与平面PMN所成角的正弦值.
查看习题详情和答案>>
( 本小题满分12分)
如图，三棱柱ABC—A1B1C1中，底面为正三角形，侧棱与底面垂直，D是BC的中点，AA1=AB=1。
（1） 求证：A1C∥平面AB1D；
（2） 求点C到平面AB1D的距离。
查看习题详情和答案>>
(本小题满分12分)
如图，已知三棱柱ABC—A1B1C1的侧棱与底面垂直，AA1＝AB＝AC＝1，AB⊥AC，M、N分别是CC1、BC的中点，点P在A1B1上，且满足＝λ(λ∈R).
(1)证明：PN⊥AM；
(2)当λ取何值时，直线PN与平面ABC所成的角θ最大？并求该最大角的正切值；
(3)若平面PMN与平面ABC所成的二面角为45°，试确定点P的位置.
查看习题详情和答案>>
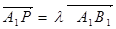
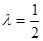，求直线AA1与平面PMN所成角的正弦值.