Question

(本小题满分12分)

如图，已知三棱柱ABC-A₁B₁C₁的侧棱与底面垂直，AA₁=AB=AC=1,且AB⊥AC，M是CC₁的中点，N是BC的中点，点P在直线A₁B₁上，且满足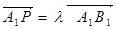

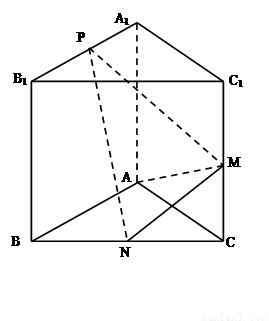
(1)证明：PN⊥AM

(2)若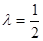，求直线AA₁与平面PMN所成角的正弦值.

 

Answer 1

【答案】

（1）根据线面垂直的性质定理来得到线线垂直。

（2）

【解析】

试题分析：解：（1）法一：取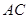中点，连,,

   

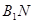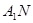
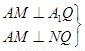
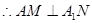
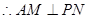
法二：建系证------------------------------（6分）

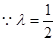
（2） 的中点

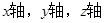以A为原点，射线,分别为的正向

建立空间直角坐标系，则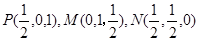

平面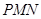的法向量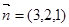  （求法向量过程略）

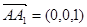
  -----------（12分）

考点：空间中线线垂直证明，以及线面角的求解

点评：解决试题的关键是能根据已知的条件得到，进而结合性质定理来得到线线垂直的证明 ，同时能建立直角坐标系的方法来求解线面角，属于基础题。