摘要：(1)设椭圆方程为． 依题意得方程组 解得. 得椭圆的方程为.---.6分 (2)如图.不妨设P点在Q点的左方且P.Q在准线上的射影分别为.. ∵|QF|＝2|PF|.设|PF|＝k.则|QF|＝2k. 由. 得到. 过P作PR⊥.则. 又有. 在中.. ∴.即∠QPR＝. 则P.Q所在的直线的斜率为. 由F(0,2)即得过P.Q的直线方程为. 当P点在Q点的右方时.则所求的直线方程为．-.12分
网址：http://m.1010jiajiao.com/timu3_id_508263[举报]
已知中心在原点，焦点在
轴上的椭圆
的离心率为
，且经过点
.
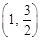（Ⅰ）求椭圆的方程；
（Ⅱ）是否存过点
（2,1）的直线
与椭圆相交于不同的两点
，满足
？若存在，求出直线的方程；若不存在，请说明理由．
【解析】第一问利用设椭圆的方程为
，由题意得
解得
第二问若存在直线满足条件的方程为
，代入椭圆的方程得
．
因为直线与椭圆相交于不同的两点，设两点的坐标分别为
，
所以
所以
．解得。
解：⑴设椭圆的方程为，由题意得
解得，故椭圆的方程为
．……………………4分
⑵若存在直线满足条件的方程为，代入椭圆的方程得
．
因为直线与椭圆相交于不同的两点，设两点的坐标分别为，
所以
所以．
又
，
因为，即
，
所以
．
即
．
所以
，解得
．
因为A,B为不同的两点，所以k=1/2．
于是存在直线L1满足条件，其方程为y=1/2x
查看习题详情和答案>>