题目内容
设椭圆方程为x2+| y2 |
| 4 |
| OP |
| 1 |
| 2 |
| OA |
| OB |
分析:设出直线l的方程,A,B的坐标,联立直线与椭圆的方程,利用韦达定理表示出x1+x2,利用直线方程表示出y1+y2,然后利用
=
(
+
)求得
的坐标,设出P的坐标,然后联立方程消去参数k求得x和y的关系式,P点轨迹可得.
| OP |
| 1 |
| 2 |
| OA |
| OB |
| OP |
解答:解:设P(x,y)是所求轨迹上的任一点,
①当斜率存在时,直线l的方程为y=kx+1,A(x1,y1),B(x2,y2),
椭圆:4x2+y2-4=0
由直线l:y=kx+1代入椭圆方程得到:
(4+k2)x2+2kx-3=0,
x1+x2=-
,y1+y2=
,
由
=
(
+
)得:
(x,y)=
(x1+x2,y1+y2),
即:
消去k得:4x2+y2-y=0
当斜率不存在时,AB的中点为坐标原点,也适合方程
所以动点P的轨迹方程为:4x2+y2-y=0.
①当斜率存在时,直线l的方程为y=kx+1,A(x1,y1),B(x2,y2),
椭圆:4x2+y2-4=0
由直线l:y=kx+1代入椭圆方程得到:
(4+k2)x2+2kx-3=0,
x1+x2=-
| 2k |
| 4+k2 |
| 8 |
| 4+k2 |
由
| OP |
| 1 |
| 2 |
| OA |
| OB |
(x,y)=
| 1 |
| 2 |
即:
|
消去k得:4x2+y2-y=0
当斜率不存在时,AB的中点为坐标原点,也适合方程
所以动点P的轨迹方程为:4x2+y2-y=0.
点评:本小题主要考查平面向量的概念、直线方程的求法、椭圆的方程和性质等基础知识,以及轨迹的求法与应用、曲线与方程的关系等解析几何的基本思想和综合解题能力.

练习册系列答案
相关题目
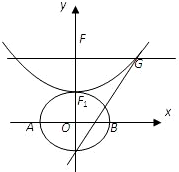 设b>0,椭圆方程为
设b>0,椭圆方程为 设b>0,椭圆方程为
设b>0,椭圆方程为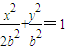 ,抛物线方程为x2=8(y-b).如图所示,过点F(0,b+2)作x轴的平行线,与抛物线在第一象限的交点为G,已知抛物线在点G的切线经过椭圆的右焦点F1.
,抛物线方程为x2=8(y-b).如图所示,过点F(0,b+2)作x轴的平行线,与抛物线在第一象限的交点为G,已知抛物线在点G的切线经过椭圆的右焦点F1. 设b>0,椭圆方程为
设b>0,椭圆方程为 ,抛物线方程为x2=8(y-b).如图所示,过点F(0,b+2)作x轴的平行线,与抛物线在第一象限的交点为G,已知抛物线在点G的切线经过椭圆的右焦点F1.
,抛物线方程为x2=8(y-b).如图所示,过点F(0,b+2)作x轴的平行线,与抛物线在第一象限的交点为G,已知抛物线在点G的切线经过椭圆的右焦点F1.