题目内容
设椭圆方程为x2+
=1,过点M(0,1)的直线l交椭圆于点A、B,O为坐标原点,点P为AB的中点,当l绕点M旋转时,求动点P的轨迹方程 .
| y2 | 4 |
分析:设出A,B两点的坐标,在设出AB中点的坐标,再设出直线l的方程,分别把A,B的坐标代入直线方程和椭圆的方程,利用点差法得到斜率和点的坐标的关系,把A,B的坐标用其中点P的坐标表示,整理后可得答案.
解答:解:设A,B点的坐标分别为(x1,y1),(x2,y2),P的坐标为(x,y).
则x=
,y=
.
设直线l的方程为y=kx+1,
把A,B坐标代入椭圆方程得x12+
=1,x22+
=1.
两式相减得(x1+x2)(x1-x2)+
=0 ①.
将A,B坐标代入直线方程得,y1=kx1+1,y2=kx2+1,
两式相减得y1-y2=k(x1-x2),代入①式得(x1-x2)[(x1+x2)+
]=0.
∵M点在椭圆里面,又椭圆与y轴的交点为(0,-2)和(0,2),∴x1-x2≠0.
即由上式可得(x1+x2)+
=0 ②.
另外将两式y1=kx1+1,y2=kx2+1相加得,
y1+y2=k(x1+x2)+2,得k=
,代入②式并整理得,
(x1+x2)2+
-
=0,即4x2+y2-y=0.
故答案为:4x2+y2-y=0.
则x=
| x1+x2 |
| 2 |
| y1+y2 |
| 2 |
设直线l的方程为y=kx+1,
把A,B坐标代入椭圆方程得x12+
| y12 |
| 4 |
| y22 |
| 4 |
两式相减得(x1+x2)(x1-x2)+
| (y1+y2)(y1-y2) |
| 4 |
将A,B坐标代入直线方程得,y1=kx1+1,y2=kx2+1,
两式相减得y1-y2=k(x1-x2),代入①式得(x1-x2)[(x1+x2)+
| k(y1+y2) |
| 4 |
∵M点在椭圆里面,又椭圆与y轴的交点为(0,-2)和(0,2),∴x1-x2≠0.
即由上式可得(x1+x2)+
| k(y1+y2) |
| 4 |
另外将两式y1=kx1+1,y2=kx2+1相加得,
y1+y2=k(x1+x2)+2,得k=
| y1+y2-2 |
| x1+x2 |
(x1+x2)2+
| (y1+y2)2 |
| 4 |
| y1+y2 |
| 2 |
故答案为:4x2+y2-y=0.
点评:本题考查了轨迹方程的求法,训练了点差法,求解过程体现了“设而不求”的解题思想方法,是中档题.

练习册系列答案
 出彩同步大试卷系列答案
出彩同步大试卷系列答案
相关题目
 设b>0,椭圆方程为
设b>0,椭圆方程为 设b>0,椭圆方程为
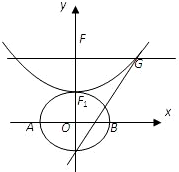
设b>0,椭圆方程为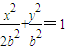 ,抛物线方程为x2=8(y-b).如图所示,过点F(0,b+2)作x轴的平行线,与抛物线在第一象限的交点为G,已知抛物线在点G的切线经过椭圆的右焦点F1.
,抛物线方程为x2=8(y-b).如图所示,过点F(0,b+2)作x轴的平行线,与抛物线在第一象限的交点为G,已知抛物线在点G的切线经过椭圆的右焦点F1. 设b>0,椭圆方程为
设b>0,椭圆方程为 ,抛物线方程为x2=8(y-b).如图所示,过点F(0,b+2)作x轴的平行线,与抛物线在第一象限的交点为G,已知抛物线在点G的切线经过椭圆的右焦点F1.
,抛物线方程为x2=8(y-b).如图所示,过点F(0,b+2)作x轴的平行线,与抛物线在第一象限的交点为G,已知抛物线在点G的切线经过椭圆的右焦点F1.