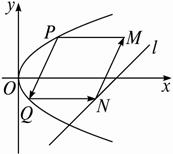
摘要:20.抛物线有光学性质.即由其焦点射出的光线经抛物线反射后.沿平行于抛物线对称轴的方向射出.如右图所示.今有抛物线.一光源在点处.由其发出的光线沿平行于抛物线的轴的方向射向抛物线上的点P.反射后.又射向抛物线上的点Q.再反射后又沿平行于抛物线的轴的方向射出.途中遇到直线上的点N.再反射后又射回点M. (1)设P.Q两点的坐标分别是. 证明:.
网址:http://m.1010jiajiao.com/timu3_id_508230[举报]
 抛物线有光学性质:由其焦点射出的光线经抛物线反象后,沿平行于抛物线对称轴的肖向射出,反之亦然.如图所示,今有抛物线C,其顶点是坐标原点,对称辅为x轴.开口向右.一光源在点M处,由其发出一条平行于x轴的光线射向抛物线C卜的点P(4.4),经抛物线C反射后,反射光线经过焦点F后射向抛物线C上的点Q,再经抛物线C反射后又沿平行于X轴的方向射出,途中经直线l:2x-4y-17=0上点N反射后又射回点M.
抛物线有光学性质:由其焦点射出的光线经抛物线反象后,沿平行于抛物线对称轴的肖向射出,反之亦然.如图所示,今有抛物线C,其顶点是坐标原点,对称辅为x轴.开口向右.一光源在点M处,由其发出一条平行于x轴的光线射向抛物线C卜的点P(4.4),经抛物线C反射后,反射光线经过焦点F后射向抛物线C上的点Q,再经抛物线C反射后又沿平行于X轴的方向射出,途中经直线l:2x-4y-17=0上点N反射后又射回点M.(1)求抛物线C的方程;
(2)求PQ的长度;
(3)判断四边形MPQN是否为平行四边形,若是请给出证明,若不是请说明理由.
抛物线有光学性质:由其焦点射出的光线经抛物线折射后,沿平行于抛物线对称轴的方向射出。现已知抛物线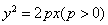 的焦点为F,过抛物线上点
的焦点为F,过抛物线上点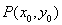 的切线为
的切线为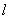 ,过P点作平行于x轴的直线m,过焦点F作平行于
,过P点作平行于x轴的直线m,过焦点F作平行于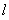 的直线交m于M,则
的直线交m于M,则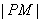 的长为( )
的长为( )
A. 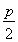 B.
B. 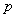 C.
C. 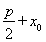 D.
D. 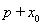
查看习题详情和答案>>
抛物线有光学性质:由其焦点射出的光线经抛物线折射后,沿平行于抛物线对称轴的方向射出。现已知抛物线 的焦点为F,过抛物线上点
的焦点为F,过抛物线上点 的切线为
的切线为 ,过P点作平行于x轴的直线m,过焦点F作平行于
,过P点作平行于x轴的直线m,过焦点F作平行于 的直线交m于M,则
的直线交m于M,则 的长为( )
的长为( )
A. | B. | C. | D. |
抛物线有光学性质: 由其焦点射出的光线经抛物线折射后,沿平行于抛物线对称轴的方向射出,今有抛物线y2=2px(p>0)![]() 一光源在点M(
一光源在点M(![]() ,4)处,由其发出的光线沿平行于抛物线的轴的方向射向抛物线上的点P,折射后又射向抛物线上的点Q,再折射后,又沿平行于抛物线的轴的方向射出,途中遇到直线l: 2x-4y-17=0上的点N,再折射后又射回点M(如下图所示)
,4)处,由其发出的光线沿平行于抛物线的轴的方向射向抛物线上的点P,折射后又射向抛物线上的点Q,再折射后,又沿平行于抛物线的轴的方向射出,途中遇到直线l: 2x-4y-17=0上的点N,再折射后又射回点M(如下图所示)

(1)设P、Q两点坐标分别为(x1,y1)、(x2,y2),证明:y1·y2=-p2;
(2)求抛物线的方程;
(3)试判断在抛物线上是否存在一点,使该点与点M关于PN所在的直线对称?若存在,请求出此点的坐标;若不存在,请说明理由.
查看习题详情和答案>>