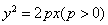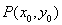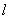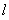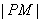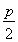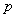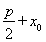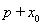��Ŀ����
�������й�ѧ���ʣ����佹������Ĺ��߾��������������ƽ���������߶Գ���ķ������������������y2=2px(p��0).һ��Դ�ڵ�M(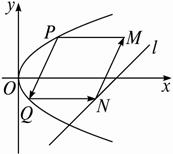
��1����P��Q��������ֱ�Ϊ(x1,y1)��(x2,y2)��֤��y1��y2=-p2��
��2���������ߵķ��̣�
��3�����ж������������Ƿ����һ�㣬ʹ�õ����M����PN���ڵ�ֱ�߶Գƣ������ڣ�������˵�����ꣻ�������ڣ���˵������.
˼·������������һ���������еĹ�ѧ֪ʶ���ϵ��ۺ�����Ŀ.
֤��:�������ߵĹ�ѧ���ʼ����⣬֪����PQ�ع������ߵĽ���F(![]() ��0)����ֱ��PQ�ķ���Ϊy=k(
��0)����ֱ��PQ�ķ���Ϊy=k(![]() ), ��
), ��
�ɢ�ʽ,��x=![]() .
.
������������߷���y2=2px�У�������y2-![]() -p2=0.��Τ�ﶨ����y1y2=-p2.
-p2=0.��Τ�ﶨ����y1y2=-p2.
��ֱ��PQ��б�ʽ�Ϊ90��ʱ����x=![]() ���������߷��̣���y=��p,ͬ���õ�y1��y2=-p2.
���������߷��̣���y=��p,ͬ���õ�y1��y2=-p2.
(2)�⣺��Ϊ����QN��ֱ��l�����������M�㣬����ֱ��MN��ֱ��QN����ֱ��l�Գ�.���M(![]() ��4)����l�ĶԳƵ�ΪM��(x��,y��)��
��4)����l�ĶԳƵ�ΪM��(x��,y��)��
�� ���
���
ֱ��QN�ķ���Ϊy=-1,Q���������y2=-1.
������P���������y1=4������(1)֪��y1��y2=-p2,��4��(-1)=-p2,��p=2.
�����������߷���Ϊy2=4x.
(3)�⣺��y=4����y2=4x,��x=4.��P������Ϊ(4��4).��y=-1����ֱ��l�ķ���Ϊ2x-4y-17=0.��x=![]() .��N������Ϊ(
.��N������Ϊ(![]() ��-1).��P��N���������ֱ��PN�ķ���Ϊ2x+y-12=0.
��-1).��P��N���������ֱ��PN�ķ���Ϊ2x+y-12=0.
��M�����ֱ��NP�ĶԳƵ�ΪM1(x1,y1)��
��
���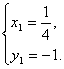
��M1(![]() ,-1)�������������߷���y2=4x�Ľ⣬
,-1)�������������߷���y2=4x�Ľ⣬
���������ϴ���һ��(![]() ��-1)���M����ֱ��PN�Գ�.
��-1)���M����ֱ��PN�Գ�.

 �¿α�����Ķ�ѵ��ϵ�д�
�¿α�����Ķ�ѵ��ϵ�д� �������й�ѧ���ʣ����佹������Ĺ��߾������߷������ƽ���������߶Գ����Ф���������֮��Ȼ����ͼ��ʾ������������C���䶥��������ԭ�㣬�ԳƸ�Ϊx�ᣮ�������ң�һ��Դ�ڵ�M�������䷢��һ��ƽ����x��Ĺ�������������C���ĵ�P��4.4������������C���������߾�������F������������C�ϵĵ�Q���پ�������C���������ƽ����X��ķ��������;�о�ֱ��l��2x-4y-17=0�ϵ�N���������ص�M��
�������й�ѧ���ʣ����佹������Ĺ��߾������߷������ƽ���������߶Գ����Ф���������֮��Ȼ����ͼ��ʾ������������C���䶥��������ԭ�㣬�ԳƸ�Ϊx�ᣮ�������ң�һ��Դ�ڵ�M�������䷢��һ��ƽ����x��Ĺ�������������C���ĵ�P��4.4������������C���������߾�������F������������C�ϵĵ�Q���پ�������C���������ƽ����X��ķ��������;�о�ֱ��l��2x-4y-17=0�ϵ�N���������ص�M��