摘要：6．(理)平面向量也叫二维向量.二维向量的坐标表示及其运算可以推广到n维向量. n维向量可用(x1.x2.x3.x4.-,xn)表示.设a=(a1, a2, a3, a4.-, an).b=(b1, b2, b3, b4,-,bn).规定向量a与b夹角θ的余弦为. 当a=.b=时.cosθ= ( ) A． B． C． D． (文)....是共起点的向量..不共线..则.. 的终点共线的充分必要条件是 ( ) A． B． C． D．
网址：http://m.1010jiajiao.com/timu3_id_507622[举报]
我们已经知道平面向量（也叫二维向量）
=（x，y）的模|
|=
，空间向量（也叫三维向量）
=（x，y，z）的模|
|=
．由此类比，n维向量
=（x1，x2，x3，…，xn）的模|
|=
．
查看习题详情和答案>>
| a |
| a |
| x 2+y2 |
| a |
| a |
| x 2+y2+z2 |
| a |
| a |
| x12+x22+x32+…+xn2 |
| x12+x22+x32+…+xn2 |
我们已经知道平面向量（也叫二维向量）
=（x，y）的模|
|=
，空间向量（也叫三维向量）
=（x，y，z）的模|
|=
．由此类比，n维向量
=（x1，x2，x3，…，xn）的模|
|=______．
查看习题详情和答案>>
| a |
| a |
| x 2+y2 |
| a |
| a |
| x 2+y2+z2 |
| a |
| a |
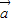=（x，y）的模
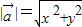，空间向量（也叫三维向量）
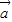=（x，y，z）的模
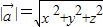．由此类比，n维向量
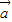=（x1，x2，x3，…，xn）的模
= ．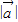