题目内容
平面向量也叫二维向量,二维向量的坐标表示及其运算可以推广到n(n≥3)维向量,n维向量可用(x1,x2,x3,x4,…,xn)表示.设
=(a1,a2,a3,a4,…,an),
=(b1,b2,b3,b4,…,bn),规定向量
与
夹角θ的余弦为cosθ=
.已知n维向量
,
,当
=(1,1,1,1,…,1),
=(-1,-1,1,1,1,…,1)时,cosθ等于
.
| a |
| b |
| a |
| b |
| ||||||||||||
|
| a |
| b |
| a |
| b |
| n-4 |
| n |
| n-4 |
| n |
分析:利用题中对向量运算的推广;利用向量的数量积公式求出两个向量的数量积;利用向量模的坐标公式求出两个向量的模;利用向量的数量积公式表示出夹角余弦,求出夹角的余弦值即可.
解答:解:由题意对运算的推广得
•
=1×(-1)+1×(-1)+1×1+…+1×1=n-4
|
|=
=
,|
|=
=
∴cosθ=
=
故答案为:
.
| a |
| b |
|
| a |
| 1+1+1+..+1 |
| n |
| b |
| 1+1+1+…+1 |
| n |
∴cosθ=
| ||||
|
|
| n-4 |
| n |
故答案为:
| n-4 |
| n |
点评:本题考查向量的数量积公式、考查向量模的公式、考查利用向量的数量积公式求向量夹角、考查新定义的题型关键是理解透新定义.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目

 =(a1,a2,a3,a4,…,an),
=(a1,a2,a3,a4,…,an), =(b1,b2,b3,b4,…,bn),规定向量
=(b1,b2,b3,b4,…,bn),规定向量 .已知n维向量
.已知n维向量 维向量,n维向量可用
维向量,n维向量可用 规定向量
规定向量
 = ( )
= ( )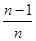 B.
B. C.
C. D.
D.