摘要:2.已知为非负数..求的最值.
网址:http://m.1010jiajiao.com/timu3_id_506229[举报]
已知函数![]() , 函数
, 函数![]() .
.
(1)若![]() 的值域为
的值域为![]() ,求实数
,求实数![]() 的取值范围;
的取值范围;
(2)当![]() 时,求函数
时,求函数![]() 的最小值
的最小值![]() ;
;
(3)是否存在非负实数m、n,使得函数![]() 的定义域为
的定义域为![]() ,值域为
,值域为![]() ,
,
若存在,求出![]() 、
、![]() 的值;若不存在,则说明理由.
的值;若不存在,则说明理由.
(1)已知矩阵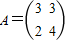 ,向量
,向量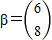 ,
,
(Ⅰ)求矩阵A的特征值和对应的特征向量;
(Ⅱ)求向量α,使得A2α=β.
(2)在直角坐标平面内,以坐标原点O为极点,x轴的非负半轴为极轴建立极坐标系.已知点A、B的极坐标分别为(1,0)、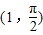 ,曲线C的参数方程为
,曲线C的参数方程为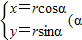 为参数,r>0)
为参数,r>0)
(Ⅰ)求直线AB的直角坐标方程;
(Ⅱ)若直线AB和曲线C只有一个交点,求r的值.
(3)设不等式|x-2|>1的解集与关于x的不等式x2-ax+b>0的解集相同.
(Ⅰ)求a,b的值;
(Ⅱ)求函数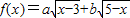 的最大值,以及取得最大值时x的值.
的最大值,以及取得最大值时x的值.
查看习题详情和答案>>
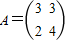 ,向量
,向量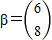 ,
,(Ⅰ)求矩阵A的特征值和对应的特征向量;
(Ⅱ)求向量α,使得A2α=β.
(2)在直角坐标平面内,以坐标原点O为极点,x轴的非负半轴为极轴建立极坐标系.已知点A、B的极坐标分别为(1,0)、
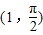 ,曲线C的参数方程为
,曲线C的参数方程为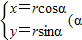 为参数,r>0)
为参数,r>0)(Ⅰ)求直线AB的直角坐标方程;
(Ⅱ)若直线AB和曲线C只有一个交点,求r的值.
(3)设不等式|x-2|>1的解集与关于x的不等式x2-ax+b>0的解集相同.
(Ⅰ)求a,b的值;
(Ⅱ)求函数
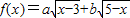 的最大值,以及取得最大值时x的值.
的最大值,以及取得最大值时x的值.查看习题详情和答案>>
(1)选修4-2:矩阵与变换
已知矩阵M=(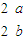 )的两^E值分别为λ1=-1和λ2=4.
)的两^E值分别为λ1=-1和λ2=4.
(I)求实数的值;
(II )求直线x-2y-3=0在矩阵M所对应的线性变换作用下的像的方程.
(2)选修4-4:坐标系与参数方程
在直角坐标平面内,以坐标原点O为极点x轴的非负半轴为极轴建立极坐标系.已知曲线C的参数方程为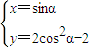 ,
,
(a为餓),曲线D的鍵标方程为ρsin(θ-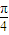 )=-
)=-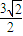 .
.
(I )将曲线C的参数方程化为普通方程;
(II)判断曲线c与曲线D的交点个数,并说明理由.
(3)选修4-5:不等式选讲
已知a,b为正实数.
(I)求证: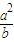 +
+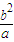 ≥a+b;
≥a+b;
(II)利用(I)的结论求函数y=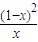 +
+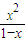 (0<x<1)的最小值.
(0<x<1)的最小值.
查看习题详情和答案>>
已知矩阵M=(
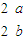 )的两^E值分别为λ1=-1和λ2=4.
)的两^E值分别为λ1=-1和λ2=4.(I)求实数的值;
(II )求直线x-2y-3=0在矩阵M所对应的线性变换作用下的像的方程.
(2)选修4-4:坐标系与参数方程
在直角坐标平面内,以坐标原点O为极点x轴的非负半轴为极轴建立极坐标系.已知曲线C的参数方程为
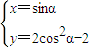 ,
,(a为餓),曲线D的鍵标方程为ρsin(θ-
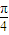 )=-
)=-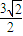 .
.(I )将曲线C的参数方程化为普通方程;
(II)判断曲线c与曲线D的交点个数,并说明理由.
(3)选修4-5:不等式选讲
已知a,b为正实数.
(I)求证:
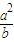 +
+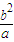 ≥a+b;
≥a+b;(II)利用(I)的结论求函数y=
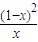 +
+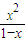 (0<x<1)的最小值.
(0<x<1)的最小值.查看习题详情和答案>>