题目内容
(1)已知矩阵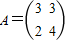 ,向量
,向量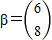 ,
,(Ⅰ)求矩阵A的特征值和对应的特征向量;
(Ⅱ)求向量α,使得A2α=β.
(2)在直角坐标平面内,以坐标原点O为极点,x轴的非负半轴为极轴建立极坐标系.已知点A、B的极坐标分别为(1,0)、
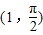 ,曲线C的参数方程为
,曲线C的参数方程为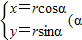 为参数,r>0)
为参数,r>0)(Ⅰ)求直线AB的直角坐标方程;
(Ⅱ)若直线AB和曲线C只有一个交点,求r的值.
(3)设不等式|x-2|>1的解集与关于x的不等式x2-ax+b>0的解集相同.
(Ⅰ)求a,b的值;
(Ⅱ)求函数
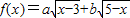 的最大值,以及取得最大值时x的值.
的最大值,以及取得最大值时x的值.
【答案】分析:(1)(Ⅰ)矩阵M的特征多项式为f(λ)=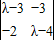 =λ2-7λ+6,令f(λ)=0,能求出矩阵M的特征值和特征向量.
=λ2-7λ+6,令f(λ)=0,能求出矩阵M的特征值和特征向量.
(Ⅱ)由矩阵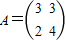 ,知A2=
,知A2= ,设向量α=
,设向量α= ,由向量
,由向量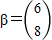 ,A2α=β,能求出向量α.
,A2α=β,能求出向量α.
(2)(Ⅰ)由点A、B的极坐标分别为(1,0)、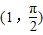 ,求出A,B的普通方程,由此能直线AB的直角坐标方程.
,求出A,B的普通方程,由此能直线AB的直角坐标方程.
(Ⅱ)由曲线C的参数方程为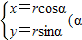 为参数,r>0),知曲线C的普通方程为x2+y2=r2.再由直线AB和曲线C只有一个交点,能求出r.
为参数,r>0),知曲线C的普通方程为x2+y2=r2.再由直线AB和曲线C只有一个交点,能求出r.
(3)(Ⅰ)解不等式|x-2|>1,不等式x2-ax+b>0的解集为{x|x>3 或x<1 }.由此能求出a和b.
(Ⅱ)由a=4,b=3,知f(x)=4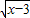 +3
+3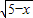 ,3≤x≤5.由(4
,3≤x≤5.由(4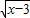 +3
+3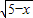 )2=7x-3+24
)2=7x-3+24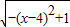 ,由此能求出f(x)的最大值为和此时x值.
,由此能求出f(x)的最大值为和此时x值.
解答:解:(1)(Ⅰ)矩阵M的特征多项式为f(λ)=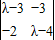 =λ2-7λ+6,
=λ2-7λ+6,
令f(λ)=0,得矩阵M的特征值为1和6.
当λ=1时,联立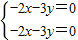 ,解得2x+3y=0
,解得2x+3y=0
所以矩阵M的属于特征值1的一个特征向量为 .
.
当λ=6时,联立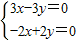 ,解得x=y
,解得x=y
所以矩阵M的属于特征值3的一个特征向量 .
.
(Ⅱ)∵矩阵 ,∴
,∴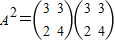 =
= ,
,
设向量α= ,∵
,∵ ,向量
,向量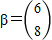 ,A2α=β,
,A2α=β,
∴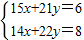 ,解得x=-1,y=1,
,解得x=-1,y=1,
∴向量α=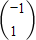 .
.
(2)(Ⅰ)∵点A、B的极坐标分别为(1,0)、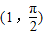 ,
,
∴点A,B的普通坐标为(1,0),(0,1),
∴直线AB的直角坐标方程为x+y-1=0.
(Ⅱ)∵曲线C的参数方程为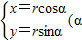 为参数,r>0),
为参数,r>0),
∴曲线C的普通方程为x2+y2=r2.
∵直线AB和曲线C只有一个交点,
∴圆心(0,0)到直线AB的距离d= =r,解得r=
=r,解得r=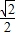 .
.
(3)(Ⅰ)解不等式|x-2|>1,得x>3 或x<1,
故不等式|x-2|>1的解集为{x|x>3 或x<1 },
由题设知不等式x2-ax+b>0的解集为{x|x>3 或x<1 }.
∴3+1=a,3×1=b
解得a=4,b=3.
(Ⅱ)∵a=4,b=3,
∴f(x)=4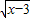 +3
+3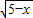 ,3≤x≤5.
,3≤x≤5.
由(4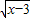 +3
+3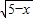 )2=16x-48+45-9x+24
)2=16x-48+45-9x+24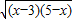
=7x-3+24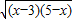
=7x-3+24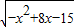
=7x-3+24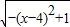
≤28-3+24=49,当且仅当x=4时取最大值.
∴f(x)的最大值为7,此时x=4.
点评:(1)考查矩阵的特征值和特征向量的求法;(2)考查极坐标与参数方程的应用;(3)考查不等式的解法及其应用.解题时要认真审题,注意挖掘题设中的隐含条件,合理地进行等价转化.
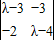 =λ2-7λ+6,令f(λ)=0,能求出矩阵M的特征值和特征向量.
=λ2-7λ+6,令f(λ)=0,能求出矩阵M的特征值和特征向量.(Ⅱ)由矩阵
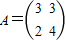 ,知A2=
,知A2= ,设向量α=
,设向量α= ,由向量
,由向量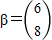 ,A2α=β,能求出向量α.
,A2α=β,能求出向量α.(2)(Ⅰ)由点A、B的极坐标分别为(1,0)、
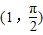 ,求出A,B的普通方程,由此能直线AB的直角坐标方程.
,求出A,B的普通方程,由此能直线AB的直角坐标方程.(Ⅱ)由曲线C的参数方程为
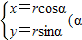 为参数,r>0),知曲线C的普通方程为x2+y2=r2.再由直线AB和曲线C只有一个交点,能求出r.
为参数,r>0),知曲线C的普通方程为x2+y2=r2.再由直线AB和曲线C只有一个交点,能求出r.(3)(Ⅰ)解不等式|x-2|>1,不等式x2-ax+b>0的解集为{x|x>3 或x<1 }.由此能求出a和b.
(Ⅱ)由a=4,b=3,知f(x)=4
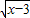 +3
+3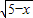 ,3≤x≤5.由(4
,3≤x≤5.由(4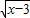 +3
+3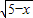 )2=7x-3+24
)2=7x-3+24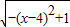 ,由此能求出f(x)的最大值为和此时x值.
,由此能求出f(x)的最大值为和此时x值.解答:解:(1)(Ⅰ)矩阵M的特征多项式为f(λ)=
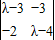 =λ2-7λ+6,
=λ2-7λ+6,令f(λ)=0,得矩阵M的特征值为1和6.
当λ=1时,联立
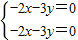 ,解得2x+3y=0
,解得2x+3y=0所以矩阵M的属于特征值1的一个特征向量为
 .
.当λ=6时,联立
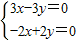 ,解得x=y
,解得x=y所以矩阵M的属于特征值3的一个特征向量
 .
.(Ⅱ)∵矩阵
 ,∴
,∴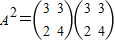 =
= ,
,设向量α=
 ,∵
,∵ ,向量
,向量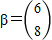 ,A2α=β,
,A2α=β,∴
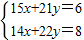 ,解得x=-1,y=1,
,解得x=-1,y=1,∴向量α=
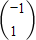 .
.(2)(Ⅰ)∵点A、B的极坐标分别为(1,0)、
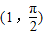 ,
,∴点A,B的普通坐标为(1,0),(0,1),
∴直线AB的直角坐标方程为x+y-1=0.
(Ⅱ)∵曲线C的参数方程为
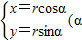 为参数,r>0),
为参数,r>0),∴曲线C的普通方程为x2+y2=r2.
∵直线AB和曲线C只有一个交点,
∴圆心(0,0)到直线AB的距离d=
 =r,解得r=
=r,解得r=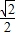 .
.(3)(Ⅰ)解不等式|x-2|>1,得x>3 或x<1,
故不等式|x-2|>1的解集为{x|x>3 或x<1 },
由题设知不等式x2-ax+b>0的解集为{x|x>3 或x<1 }.
∴3+1=a,3×1=b
解得a=4,b=3.
(Ⅱ)∵a=4,b=3,
∴f(x)=4
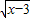 +3
+3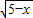 ,3≤x≤5.
,3≤x≤5.由(4
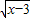 +3
+3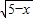 )2=16x-48+45-9x+24
)2=16x-48+45-9x+24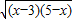
=7x-3+24
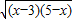
=7x-3+24
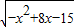
=7x-3+24
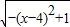
≤28-3+24=49,当且仅当x=4时取最大值.
∴f(x)的最大值为7,此时x=4.
点评:(1)考查矩阵的特征值和特征向量的求法;(2)考查极坐标与参数方程的应用;(3)考查不等式的解法及其应用.解题时要认真审题,注意挖掘题设中的隐含条件,合理地进行等价转化.

练习册系列答案
相关题目
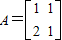 ,向量
,向量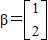 .求向量α,使得A2α=β.
.求向量α,使得A2α=β. ,点P(x,y)是椭圆上的点,若
,点P(x,y)是椭圆上的点,若 的最大值为10,求椭圆的标准方程.
的最大值为10,求椭圆的标准方程.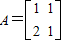 ,向量
,向量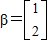 .求向量α,使得A2α=β.
.求向量α,使得A2α=β. ,点P(x,y)是椭圆上的点,若
,点P(x,y)是椭圆上的点,若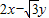 的最大值为10,求椭圆的标准方程.
的最大值为10,求椭圆的标准方程.