摘要:8.把=3x的反函数图象向右平移2个单位就得到曲线C.函数的图象与曲 线C关于成轴对称.那么等于 ( ) A. B. C. D.
网址:http://m.1010jiajiao.com/timu3_id_505887[举报]
已知函数f(x)=sin(π-
)cos
+cos2
-
,(ω>0)
(1)若函数y=f(x)的周期为π,将函数y=f(x)的图象上各点的横坐标缩短为原来的
倍(纵坐标不变),再把所得的函数图象向右平移
个单位得到函数y=g(x)的图象,求y=g(x)解析式,并求其对称中心.
(2)若函数y=f(x)在[
,π]上是减函数,求ω的取值范围.
查看习题详情和答案>>
| ωx |
| 2 |
| ωx |
| 2 |
| ωx |
| 2 |
| 1 |
| 2 |
(1)若函数y=f(x)的周期为π,将函数y=f(x)的图象上各点的横坐标缩短为原来的
| 1 |
| 2 |
| π |
| 8 |
(2)若函数y=f(x)在[
| π |
| 2 |
已知函数f(x)=sin(π-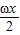 )cos
)cos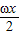 +cos2
+cos2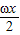
 ,(ω>0)
,(ω>0)
(1)若函数y=f(x)的周期为π,将函数y=f(x)的图象上各点的横坐标缩短为原来的 倍(纵坐标不变),再把所得的函数图象向右平移
倍(纵坐标不变),再把所得的函数图象向右平移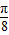 个单位得到函数y=g(x)的图象,求y=g(x)解析式,并求其对称中心.
个单位得到函数y=g(x)的图象,求y=g(x)解析式,并求其对称中心.
(2)若函数y=f(x)在[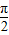 ,π]上是减函数,求ω的取值范围.
,π]上是减函数,求ω的取值范围.
查看习题详情和答案>>
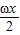 )cos
)cos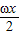 +cos2
+cos2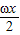
 ,(ω>0)
,(ω>0)(1)若函数y=f(x)的周期为π,将函数y=f(x)的图象上各点的横坐标缩短为原来的
 倍(纵坐标不变),再把所得的函数图象向右平移
倍(纵坐标不变),再把所得的函数图象向右平移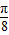 个单位得到函数y=g(x)的图象,求y=g(x)解析式,并求其对称中心.
个单位得到函数y=g(x)的图象,求y=g(x)解析式,并求其对称中心.(2)若函数y=f(x)在[
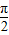 ,π]上是减函数,求ω的取值范围.
,π]上是减函数,求ω的取值范围.查看习题详情和答案>>
已知函数f(x)=sin(π-
)cos
+cos2
-
,(ω>0)
(1)若函数y=f(x)的周期为π,将函数y=f(x)的图象上各点的横坐标缩短为原来的
倍(纵坐标不变),再把所得的函数图象向右平移
个单位得到函数y=g(x)的图象,求y=g(x)解析式,并求其对称中心.
(2)若函数y=f(x)在[
,π]上是减函数,求ω的取值范围.
查看习题详情和答案>>
| ωx |
| 2 |
| ωx |
| 2 |
| ωx |
| 2 |
| 1 |
| 2 |
(1)若函数y=f(x)的周期为π,将函数y=f(x)的图象上各点的横坐标缩短为原来的
| 1 |
| 2 |
| π |
| 8 |
(2)若函数y=f(x)在[
| π |
| 2 |
 (2007•金山区一模)(1)已知平面上两定点A(-2,0)、B(2,0),且动点M的坐标满足
(2007•金山区一模)(1)已知平面上两定点A(-2,0)、B(2,0),且动点M的坐标满足| MA |
| MB |
(2)若把(1)的M的轨迹图象向右平移一个单位,再向下平移一个单位,恰与直线x+ky-3=0 相切,试求实数k的值;
(3)如图1,l是经过椭圆
| x2 |
| a2 |
| y2 |
| b2 |
| c |
| b |
| x2 |
| a2 |
| y2 |
| b2 |