摘要:16. 已知等比数的首项.数列满足首项b1=a(a为常数).且 (1)求数列的通项公式, (2)求数列的前n项和Sn. 17. 如图.四棱锥P-ABCD的底面是正方形,PA⊥底面ABCD.PA=AD=2.点M.N分别为棱PD.PC的中点. (1)求证:PD⊥平面AMN, (2)求三棱锥P-AMN的体积, (3)求二面角P-AN-M的大小.
网址:http://m.1010jiajiao.com/timu3_id_505306[举报]
.(本小题满分14分)已知等比数列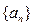 的公比为
的公比为 ,首项为
,首项为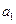 ,其前
,其前 项的和为
项的和为 .数列
.数列 的前
的前 项的和为
项的和为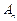 , 数列
, 数列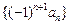 的前
的前 项的和为
项的和为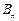
(Ⅰ)若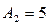 ,
,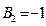 ,求
,求 的通项公式;(Ⅱ)①当
的通项公式;(Ⅱ)①当 为奇数时,比较
为奇数时,比较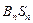 与
与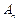 的大小; ②当
的大小; ②当 为偶数时,若
为偶数时,若 ,问是否存在常数
,问是否存在常数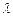 (与n无关),使得等式
(与n无关),使得等式 恒成立,若存在,求出
恒成立,若存在,求出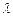 的值;若不存在,说明理由
的值;若不存在,说明理由
.(本小题满分14分)已知等比数列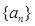 的公比为
的公比为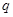 ,首项为
,首项为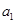 ,其前
,其前 项的和为
项的和为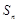 .数列
.数列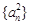 的前
的前 项的和为
项的和为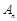 ,
数列
,
数列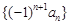 的前
的前 项的和为
项的和为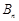
(Ⅰ)若 ,
, ,求
,求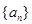 的通项公式;(Ⅱ)①当
的通项公式;(Ⅱ)①当 为奇数时,比较
为奇数时,比较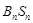 与
与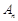 的大小;
②当
的大小;
②当 为偶数时,若
为偶数时,若 ,问是否存在常数
,问是否存在常数 (与n无关),使得等式
(与n无关),使得等式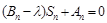 恒成立,若存在,求出
恒成立,若存在,求出 的值;若不存在,说明理由
的值;若不存在,说明理由
查看习题详情和答案>>
.(本小题满分14分)已知等比数列 的公比为
的公比为 ,首项为
,首项为 ,其前
,其前 项的和为
项的和为 .数列
.数列 的前
的前 项的和为
项的和为 ,
数列
,
数列 的前
的前 项的和为
项的和为
(Ⅰ)若 ,
, ,求
,求 的通项公式;(Ⅱ)①当
的通项公式;(Ⅱ)①当 为奇数时,比较
为奇数时,比较 与
与 的大小;
②当
的大小;
②当 为偶数时,若
为偶数时,若 ,问是否存在常数
,问是否存在常数 (与n无关),使得等式
(与n无关),使得等式 恒成立,若存在,求出
恒成立,若存在,求出 的值;若不存在,说明理由
的值;若不存在,说明理由
查看习题详情和答案>>
 的公比为
的公比为 ,首项为
,首项为 ,其前
,其前 项的和为
项的和为 .数列
.数列 的前
的前 , 数列
, 数列 的前
的前
 ,
, ,求
,求 的通项公式;(Ⅱ)①当
的通项公式;(Ⅱ)①当 与
与 的大小; ②当
的大小; ②当 ,问是否存在常数
,问是否存在常数 (与n无关),使得等式
(与n无关),使得等式 恒成立,若存在,求出
恒成立,若存在,求出