摘要：13．函数在区间的最大值为 .最小值为 . 曲线在点P处的切线和直线垂直, 则点P的坐标为 ,切线方程为 .
网址：http://m.1010jiajiao.com/timu3_id_504529[举报]
已知函数f（x）=x+
…+
，g（x）=
+
…+
，定义域为R，m，n∈N•，h1（x）=c+f（x）-g（x），h2（x）=c-f（x）+g（x）
（1）若n=1，m=2，求h1（x）的单调区间；若n=2，m=2，求h2（x）的最小值．
（2）（文科选做）若m=n，c=0时，令T（n）=h2（1），求T（n）的最大值．
（理科选做）若m=n，c=0时，令T（n）=h1（1），求证：T（n）=
+
+…+
．
（3）若m=n+1，c=1时，F（x）=h1（x+3）h2（x-2）且函数F（x）的零点均在区间[a，b]（a＜b，a，b∈Z）内，求b-a的最小值．
查看习题详情和答案>>
| x3 |
| 3 |
| x2m-1 |
| 2m-1 |
| x2 |
| 2 |
| x4 |
| 4 |
| x2n |
| 2n |
（1）若n=1，m=2，求h1（x）的单调区间；若n=2，m=2，求h2（x）的最小值．
（2）（文科选做）若m=n，c=0时，令T（n）=h2（1），求T（n）的最大值．
（理科选做）若m=n，c=0时，令T（n）=h1（1），求证：T（n）=
| 1 |
| n+1 |
| 1 |
| n+2 |
| 1 |
| 2n |
（3）若m=n+1，c=1时，F（x）=h1（x+3）h2（x-2）且函数F（x）的零点均在区间[a，b]（a＜b，a，b∈Z）内，求b-a的最小值．
已知函数f（x）=x+
…+
，g（x）=
+
…+
，定义域为R，m，n∈N•，h1（x）=c+f（x）-g（x），h2（x）=c-f（x）+g（x）
（1）若n=1，m=2，求h1（x）的单调区间；若n=2，m=2，求h2（x）的最小值．
（2）（文科选做）若m=n，c=0时，令T（n）=h2（1），求T（n）的最大值．
（理科选做）若m=n，c=0时，令T（n）=h1（1），求证：T（n）=
+
+…+
．
（3）若m=n+1，c=1时，F（x）=h1（x+3）h2（x-2）且函数F（x）的零点均在区间[a，b]（a＜b，a，b∈Z）内，求b-a的最小值．
查看习题详情和答案>>
| x3 |
| 3 |
| x2m-1 |
| 2m-1 |
| x2 |
| 2 |
| x4 |
| 4 |
| x2n |
| 2n |
（1）若n=1，m=2，求h1（x）的单调区间；若n=2，m=2，求h2（x）的最小值．
（2）（文科选做）若m=n，c=0时，令T（n）=h2（1），求T（n）的最大值．
（理科选做）若m=n，c=0时，令T（n）=h1（1），求证：T（n）=
| 1 |
| n+1 |
| 1 |
| n+2 |
| 1 |
| 2n |
（3）若m=n+1，c=1时，F（x）=h1（x+3）h2（x-2）且函数F（x）的零点均在区间[a，b]（a＜b，a，b∈Z）内，求b-a的最小值．
已知φ(x)=
，a为正常数．（e=2.71828…）；
（理科做）（1）若f(x)=lnx+φ(x)，且a=
，求函数f（x）在区间[1，e]上的最大值与最小值
（2）若g（x）=|lnx|+φ（x），且对任意x1，x2∈（0，2]，x1≠x2都有
＜-1，求a的取值范围．
（文科做）（1）当a=2时描绘?（x）的简图
（2）若f(x)=?(x)+
，求函数f（x）在区间[1，e]上的最大值与最小值．
查看习题详情和答案>>
| a |
| x+1 |
（理科做）（1）若f(x)=lnx+φ(x)，且a=
| 9 |
| 2 |
（2）若g（x）=|lnx|+φ（x），且对任意x1，x2∈（0，2]，x1≠x2都有
| g(x2)-g(x1) |
| x2-x1 |
（文科做）（1）当a=2时描绘?（x）的简图
（2）若f(x)=?(x)+
| 1 |
| ?(x) |
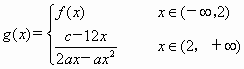为连续函数，求c的值．
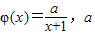为正常数．（e=2.71828…）；
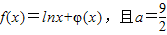，求函数f（x）在区间[1，e]上的最大值与最小值
，求a的取值范围．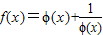
，求函数f（x）在区间[1，e]上的最大值与最小值．