摘要:19.已知函数的图象与y轴的交点为P.且曲线在P点处的切线方程为24x + y –12 = 0.若函数在 x = 2 处取得极值 –16. (1) 求f (x)的解析式, (2) 确定f (x)的单调递减区间. .解:(1)切线方程为:与y轴的交点为p代入得d=12----.------..2分 -------------..-..4分 ----------..-..5分 又因函数f(x)在x=2处的极值为-16 ------..-..9分 知:令-..-11分 所以原函数的单调递减区间为------.12分
网址:http://m.1010jiajiao.com/timu3_id_504308[举报]
已知函数y=x2(x>0)的图象在点(ak,ak2)处的切线与x轴的交点的横坐标为ak+1(k∈N*),a1=1;数列{bn}满足:b1=2,且对任意p,q∈N*,都有bp+bq=bp+q.
(I)求数列{an}、{bn}的通项公式;
(II)求数列{an•bn}的前n项和Tn. 查看习题详情和答案>>
(I)求数列{an}、{bn}的通项公式;
(II)求数列{an•bn}的前n项和Tn. 查看习题详情和答案>>

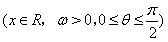 的图象与y轴相交于点
的图象与y轴相交于点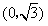 ,且该函数的最小正周期为
,且该函数的最小正周期为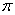 。
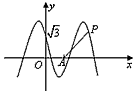
。 
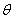 和
和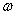 的值;
的值; ,点P是该函数图象上一点,点
,点P是该函数图象上一点,点 是PA的中点,当
是PA的中点,当 ,
,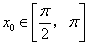 时,求
时,求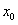 的值。
的值。 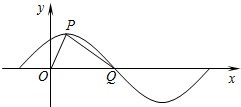 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,0<φ<
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,0<φ<