题目内容
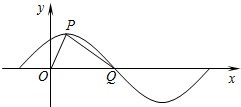 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,0<φ<
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,0<φ<| π |
| 2 |
| ||
| 2 |
| ||
| 2 |
(Ⅰ)求函数y=f(x)的解析式;
(Ⅱ)将函数y=f(x)图象向右平移1个单位后得到函数y=g(x)的图象,当x∈[0,2]时,求函数h(x)=f(x)•g(x)的最大值.
分析:(Ⅰ)由余弦定理得cos∠POQ 的值,可得sin∠POQ,求出P的坐标可得A的值,再由函数的周期求出ω的值,再把点P的坐标代入函数解析式求出φ,即可求得 y=f(x) 的解析式.
(Ⅱ)求出g(x) 的解析式,化简h(x)=f(x)g(x) 的解析式为
sin(
x-
)+
,再根据x的范围求出h(x) 的值域,从而求得h(x) 的最大值.
(Ⅱ)求出g(x) 的解析式,化简h(x)=f(x)g(x) 的解析式为
| 1 |
| 2 |
| 2π |
| 3 |
| π |
| 6 |
| 1 |
| 4 |
解答:解:(Ⅰ)由余弦定理得cos∠POQ=
=
,…(2分)
∴sin∠POQ=
,得P点坐标为(
,1),∴A=1,
=4(2-
),∴ω=
. …(5分)
由f(
)=sin(
+φ)=1 可得 φ=
,∴y=f(x) 的解析式为 f(x)=sin(
x+
).…(6分)
(Ⅱ)根据函数y=Asin(ωx+∅)的图象变换规律求得 g(x)=sin
x,…(7分)
h(x)=f(x)g(x)=sin(
x+
) sin
x=
sin2
x+
sin
xcos
x
=
+
sin
x=
sin(
x-
)+
.…(10分)
当x∈[0,2]时,
x -
∈[-
,
],
∴当
x -
=
,
即 x=1时,hmax(x)=
.…(12分)
| ||||||
2|
|
| ||
| 5 |
∴sin∠POQ=
2
| ||
| 5 |
| 1 |
| 2 |
| 2π |
| ω |
| 1 |
| 2 |
| π |
| 3 |
由f(
| 1 |
| 2 |
| π |
| 6 |
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
(Ⅱ)根据函数y=Asin(ωx+∅)的图象变换规律求得 g(x)=sin
| π |
| 3 |
h(x)=f(x)g(x)=sin(
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
| 1 |
| 2 |
| π |
| 3 |
| ||
| 2 |
| π |
| 3 |
| π |
| 3 |
=
1-cos
| ||
| 4 |
| ||
| 4 |
| 2π |
| 3 |
| 1 |
| 2 |
| 2π |
| 3 |
| π |
| 6 |
| 1 |
| 4 |
当x∈[0,2]时,
| 2π |
| 3 |
| π |
| 6 |
| π |
| 6 |
| 7π |
| 6 |
∴当
| 2π |
| 3 |
| π |
| 6 |
| π |
| 2 |
即 x=1时,hmax(x)=
| 3 |
| 4 |
点评:本题主要考查由函数y=Asin(ωx+∅)的部分图象求函数的解析式,函数y=Asin(ωx+∅)的图象变换规律,正弦函数的定义域和值域,属于中档题.

练习册系列答案
 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目