摘要： 已知Sn为数列{an}的前n项和. = (, 2)与 = (-1, 1)共线 (1) 求数列{n}的前 n项和 (2)若对任意nN* .K+≤4+14成立.试求实数K的最大值.
网址：http://m.1010jiajiao.com/timu3_id_503829[举报]
(本小题满分12分)
已知Sn为数列{an}的前n项和，a1=9,Sn=n2an-n2(n-1),设bn=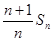
(1)求证：bn-bn-1="n" (n≥2，n∈N).
(2)求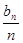
的最小值.
查看习题详情和答案>>
(本小题满分12分)
已知Sn为数列{an}的前n项和，a1=9,Sn=n2an-n2(n-1),设bn=
(1)求证：bn-bn-1="n" (n≥2，n∈N).
(2)求
的最小值.
(本小题满分12分)
已知Sn为数列{an}的前n项和，a1=9,Sn=n2an-n2(n-1),设bn=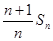
(1)求证：bn-bn-1="n" (n≥2，n∈N).
(2)求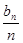
的最小值.
已知Sn为数列{an}的前n项和，a1=9,Sn=n2an-n2(n-1),设bn=
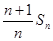
(1)求证：bn-bn-1="n" (n≥2，n∈N).
(2)求
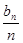的最小值.
n项和为Sn，且a3=5，S15="225." 
+2n，求数列{bn}的前n项和Tn.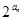 
+2n，求数列{bn}的前n项和Tn.