摘要：46．(2005湖南卷理第19题.文第21题.满分14分) 已知椭圆C:+＝1(a＞b＞0)的左．右焦点为F1.F2.离心率为e. 直线l:y＝ex+a与x轴．y轴分别交于点A.B.M是直线l与椭圆C的一个公共点.P是点F1关于直线l的对称点.设＝λ. (Ⅰ)证明:λ＝1-e2, (Ⅱ)若.△PF1F2的周长为6,写出椭圆C的方程, (Ⅲ)确定λ的值.使得△PF1F2是等腰三角形.
网址：http://m.1010jiajiao.com/timu3_id_503553[举报]
已知椭圆x2＋
＝1的左、右两个顶点分别为A，B.双曲线C的方程为x2－＝1. 设点P在第一象限且在双曲线C上，直线AP与椭圆相交于另一点T.
(Ⅰ)设P, T两点的横坐标分别为x1，x2，证明x1· x2＝1；
(Ⅱ)设△TAB与△POB(其中O为坐标原点)的面积分别为S1与S2 ，且
·
≤15，求S
－S
的取值范围．
已知椭圆E：
＝1的左焦点为F，左准线l与x轴的交点是圆C的圆心，圆C恰好经过坐标原点O，设G是圆C上任意一点．
(1)求圆C的方程；
(2)若直线FG与直线l交于点T，且G为线段FT的中点，求直线FG被圆C所截得的弦长；
(3)在平面上是否存在一点P，使得
？若存在，求出点P坐标；若不存在，请说明理由．
已知函数f(x)＝－x3＋ax2＋b(a，b∈R)．
(1)求函数f(x)的单调递增区间；
(2)若对任意a∈[3，4]，函数f(x)在R上都有三个零点，求实数b的取值范围．
已知椭圆x2＋
＝1的左、右两个顶点分别为A、B．曲线C是以A、B两点为顶点，离心率为
的双曲线，设点P在第一象限且在曲线C上，直线AP与椭圆相交于另一点T．
(1)求曲线C的方程；
(2)设点P、T的横坐标分别为x1，x2，证明：x1·x2＝1；
(3)设△TAB与△POB(其中O为坐标原点)的面积分别为S1与S2，且
，求S
－S
的取值范围．
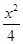＋y2＝1的左顶点为A，过A作两条互相垂直的弦AM、AN交椭圆于M、N两点．
＝1(a>b>0)的离心率e＝
，一条准线方程为x＝