摘要:若是数列的前n项和.= .则= 14若x,y 满足 则z=x+2y的最大值为
网址:http://m.1010jiajiao.com/timu3_id_503478[举报]
有下列说法
①若数列〔an〕的前n项和是Sn=an2+bn+c,其中abc是常数,则数列〔an〕一定不是等差数列:
②若
=3
,
=-2
,且|
|=|
|,则四边形ABCD是等腰梯形;
③“x=-1”是“x2-5x-6=0”的必要不充分条件;
④用数学归纳法证明命题:
+
+
+…+
<1,在第二步由n=k到n=k+1时,不等式左边增加了l项.
其中正确说法的序号是 .
查看习题详情和答案>>
①若数列〔an〕的前n项和是Sn=an2+bn+c,其中abc是常数,则数列〔an〕一定不是等差数列:
②若
| AB |
| a |
| CD |
| a |
| AD |
| BC |
③“x=-1”是“x2-5x-6=0”的必要不充分条件;
④用数学归纳法证明命题:
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 8 |
| 1 |
| 2n |
其中正确说法的序号是
(本题满分14分)
(理)已知数列{an}的前n项和 ,且
,且 =1,
=1,
 .
.
(I)求数列{an}的通项公式;
(II)已知定理:“若函数f(x)在区间D上是凹函数,x>y(x,y∈D),且f’(x)存在,则有
< f’(x)”.若且函数y=xn+1 在(0,+∞)上是凹函数,试判断bn与bn+1的大小;
在(0,+∞)上是凹函数,试判断bn与bn+1的大小;
(III)求证: ≤bn<2.
≤bn<2.
查看习题详情和答案>>
(本题满分14分)
(理)已知数列{an}的前n项和 ,且
,且 =1,
=1,
 .(I)求数列{an}的通项公式;
.(I)求数列{an}的通项公式;
(II)已知定理:“若函数f(x)在区间D上是凹函数,x>y(x,y∈D),且f’(x)存在,则有
< f’(x)”.若且函数y=xn+1 在(0,+∞)上是凹函数,试判断bn与bn+1的大小;
在(0,+∞)上是凹函数,试判断bn与bn+1的大小;
(III)求证:≤bn<2.
查看习题详情和答案>>
 知数列{an}的前n项和
知数列{an}的前n项和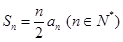 ,且
,且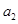 =1,
=1,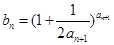
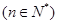 .(I)求数列{an}的通项公式;
.(I)求数列{an}的通项公式;