摘要:21. 在数列中.为其前n项和.已知且() (1)证明数列为等比数列,(2)求数列的通项公式,(3)计算 ,
网址:http://m.1010jiajiao.com/timu3_id_503107[举报]
(本小题满分12分)
在某校组织的一次篮球定点投篮训练中,规定每人最多投3次;在A处每投进一球得3分,在B处每投进一球得2分;如果前两次得分之和超过3分即停止投篮,否则投第三次,某同学在A处的命中率q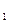 为0.25,在B处的命中率为q
为0.25,在B处的命中率为q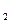 ,该同学选择先在A处投一球,以后都在B处投,用
,该同学选择先在A处投一球,以后都在B处投,用 表示该同学投篮训练结束后所得的总分,其分布列为
表示该同学投篮训练结束后所得的总分,其分布列为
(1) 求q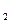 的值;
的值;
(2) 求随机变量 的数学期望E
的数学期望E ;
;
(3) 试比较该同学选择都在B处投篮得分超过3分与选择上述方式投篮得分超过3分的概率的大小。
在某校组织的一次篮球定点投篮训练中,规定每人最多投3次;在A处每投进一球得3分,在B处每投进一球得2分;如果前两次得分之和超过3分即停止投篮,否则投第三次,某同学在A处的命中率q
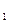 为0.25,在B处的命中率为q
为0.25,在B处的命中率为q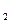 ,该同学选择先在A处投一球,以后都在B处投,用
,该同学选择先在A处投一球,以后都在B处投,用 表示该同学投篮训练结束后所得的总分,其分布列为
表示该同学投篮训练结束后所得的总分,其分布列为  | 0 | 2 | 3 | 4 | 5 |
| p | 0.03 | P1 | P2 | P3 | P4 |
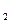 的值;
的值; (2) 求随机变量
 的数学期望E
的数学期望E ;
;(3) 试比较该同学选择都在B处投篮得分超过3分与选择上述方式投篮得分超过3分的概率的大小。
本小题满分12分)
在下表中,每行上的数从左到右都成等比数列,并且所有公比都等于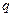 ,每列上的数从上到下都成等差数列,正数
,每列上的数从上到下都成等差数列,正数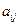 表示位于第
表示位于第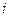 行第
行第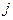 列的数,其中
列的数,其中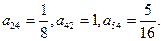
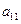 | 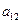 | 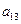 | 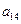 | … | 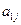 | … |
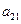 | 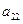 | 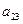 | 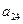 | … | 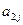 | … |
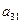 | 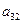 | 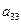 | 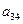 | … | 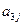 | … |
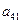 | 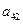 | 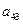 | 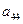 | … | 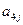 | … |
| … | … | … | … | … | … | … |
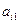 | 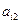 | 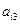 | 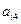 | … | 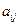 | … |
| … | … | … | … | … | … | … |
(Ⅰ)求
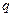 的值;
的值;(Ⅱ)求
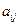 的计算公式;
的计算公式;(Ⅲ)设数列
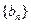 满足
满足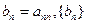 的前
的前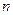 项和为
项和为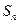 ,
,试比较
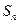 与
与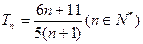 的大小,并说明理由。
查看习题详情和答案>>
的大小,并说明理由。
查看习题详情和答案>>
(本小题满分12分)(文科做前 两问;理科全做.)
两问;理科全做.)
某会议室用3盏灯照明,每盏灯各使用节能灯棍一只,且型号相同.假定每盏灯能否正常照明只与灯棍的寿命有关,该型号的灯棍寿命为1年以上的概率为0.8,寿命为2年以上的概率为0.3,从使 用之日起每满1年进行一次灯棍更换工作,只更换已坏的灯棍,平时不换.
用之日起每满1年进行一次灯棍更换工作,只更换已坏的灯棍,平时不换.
(I)在第一次灯棍更换工作中,求不需要更换灯棍的概率;
(I I)在第二次灯棍更换工作中,对其中的某一盏灯来说,求该灯需要更换灯棍的概率;
I)在第二次灯棍更换工作中,对其中的某一盏灯来说,求该灯需要更换灯棍的概率;
(III)设在第二次灯棍更换工作中,需要更换的灯棍数为ξ,求ξ的分布列和期望.
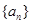 是公差不为
是公差不为 的等差数列,其前
的等差数列,其前 项和为
项和为 ,且
,且 成等比数列.
成等比数列. ,使
,使 仍为数列
仍为数列